NAS

NAS综述

1.NAS综述

AutoML（automated machine learning）是模型选择、特征提取和超参数调优的一系列自动化方法，可以实现自动训练有价值的模型。

深度学习可以自动学习出有用的特征，脱离了对特征工程的依赖，在图像、语音等任务上取得了超越其他算法的结果。这种成功很大程度上得益于新神经网络结构的出现，如ResNet、Inception、DenseNet等。但设计出高性能的神经网络需要大量的专业知识与反复实验，成本极高，限制了神经网络在很多问题上的应用。神经结构搜索（Neural Architecture Search ，简称NAS）是一种自动设计神经网络的技术，可以通过算法根据样本集自动设计出高性能的网络结构，在某些任务上甚至可以媲美人类专家的水准，甚至发现某些人类之前未曾提出过的网络结构，这可以有效的降低神经网络的使用和实现成本。

NAS的原理是给定一个称为搜索空间的候选神经网络结构集合，用某种策略从中搜索出最优网络结构。神经网络结构的优劣即性能用某些指标如精度、速度来度量，称为性能评估。

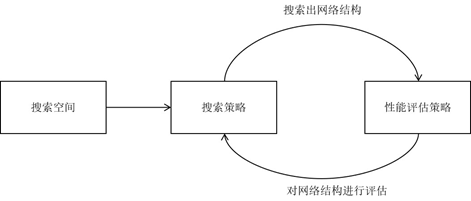
在搜索的每次迭代中，从搜索空间产生“样本”即得到一个神经网络结构，称为“子网络”。在训练样本集上训练子网络，然后在验证集上评估其性能。逐步优化网络结构，知道找到最优子结构。

搜索空间、搜索策略、性能评估策略是NAS算法的核心要素。搜索空间定义了可以搜索的神经网络结构的集合，即解的空间。搜索策略定义了如何在搜索空间中寻找最有网络结构。性能评估策略定义了如何评估搜索出的网络结构的性能。对这些要素的不同实现得到了各种不同的NAS算法。

空间

搜索空间定义了NAS算法可以搜索的神经网络的类型，同时也定义了如何描述神经网络。神经网络所实现的计算可以抽象成一个无孤立节点的有向无环图（DAG），图的节点代表神经网络的层，边代表数据的流动。每个节点从其前驱节点（有边射入）接收数据，经过计算之后将数据输出到后续节点（有边射出）。理论上说，只要是无孤立节点的DAG，都是合法的神经网络结构。按照不同的尺度，神经网络的结构定义包含如下层次的信息：

• 网络的拓扑结构

  网络有多少个层，这些层的连接关系。从简单的图结构到任意的DAG也反映了整个神经网络结构的发展历程。最简单的神经网络是线性链式结构，其对应的图的每个节点最多只有一个前驱，一个后续，类似于数据结构中的链表。早期的全连接神经网络，卷积神经网络都是这种拓扑结构。Inception、ResNet、DenseNet中的节点允许有多个前驱，多个后续，从而形成了多分支、跨层连接结构，它们是更复杂的图。这些典型的拓扑结构如下图所示。

  

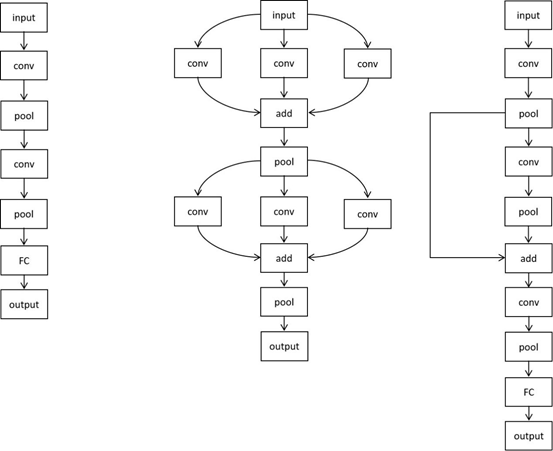
  在描述网络的拓扑结构时，一般采用前驱节点来定义，即定义每个节点的前驱节点，一旦该信息确定，则网络拓扑结构确定。

• 每个层的类型。

  除了第一个层必须为输入层，最后一个层必须为输出之外，中间的层的类型是可选的，它们代表了各种不同的运算即层的类型。典型有全连接，卷积，反卷积，空洞卷积，池化，激活函数等。但这些层的组合使用一般要符合某些规则。

• 每个层内部的超参数

  卷积层的超参数有卷积核的数量，卷积核的通道数，高度，宽度，水平方向的步长，垂直方向的步长等。全连接层的超参数有神经元的数量。激活函数层的超参数有激活函数的类型，函数的参数（如果有）等。各种典型层的超参数如下表所示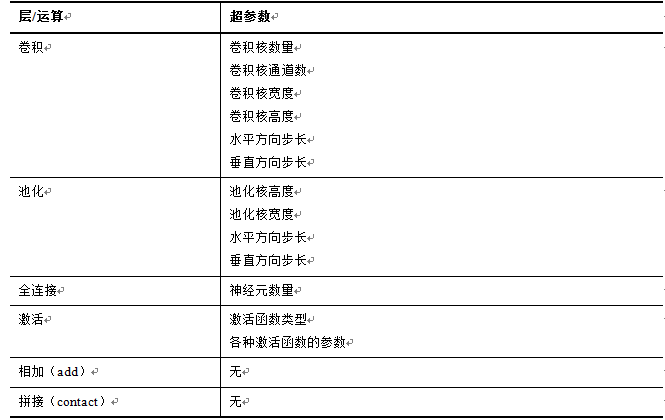

  

​ 如果一个节点的前驱节点只有一个，则直接以前驱节点的输出值作为本节点的输入。如果前驱节点有多个，需要将前驱节点的值汇总后输入本节点，这里有两种策略：相加和拼接，前者的典型代表是ResNet，后者的典型代表是DenseNet。由于神经网络的层数不固定，每层的超参数数量也不固定，因此描述网络结构的参数是变长的。

​ 为了提高搜索效率，有时候会对搜索空间进行限定或简化。在某些NAS实现中会把网络切分成基本单元（cell，或block），通过这些单元的堆叠形成更复杂的网络。基本单元由多个节点（神经网络的层）组成，它们在整个网络中重复出现多次，但具有不同的权重参数。另外一种做法是限定神经网络的整体拓扑结构，借鉴于人类设计神经网络的经验。这些做法虽然减少了NAS算法的计算量，但也限定了算法能够寻找的神经网络的类型。

​ 由于描述神经网络结构的参数含有离散数据（如拓扑结构的定义，层的类型，层内的离散型超参数），因此网络结构搜索是一个离散优化问题。定义结构的参数数量一般比较大，因此属于高维优化问题。另外，对于该问题，算法不知道优化目标函数的具体形式（每种网络结构与该网络的性能的函数关系），因此属于黑盒优化问题。这些特点为NAS带来了巨大的挑战。

搜索策略

搜索策略定义了如何找到最优的网络结构，通常是一个迭代优化过程，本质上是超参数优化问题。目前已知的搜索方法有随机搜索，贝叶斯优化，遗传算法，强化学习，基于梯度的算法。其中强化学习，遗传学习，基于梯度的优化是目前的主流算法，也是本章介绍的重点。

强化学习

​ 基于强化学习的NAS算法[4-6]将神经网络结构设计看作一个强化学习问题，学习得到一个产生网络结构的最优策略。这里的智能体是设计神经网络结构的算法，用于输出神经网络结构描述，强化学习算法使得生成的神经网络的性能最优化。为了用强化学习求解，可以将神经网络的设计看做一个动作序列，每次执行动作确定网络的一部分结构如层。神经网络在验证集上的性能值是强化学习中的奖励值。

​ 由于神经网络的结构参数长度不固定，因此需要用一个可变长度的串描述网络结构，算法需要输出这种不定长的串。循环神经网络可以输出不固定长度是数据，因此可以用它来生成网络结构的描述，文献[2]提出的NAS采用了这种方案。

​ 算法用一个称为控制器的循环神经网络生成描述子网络结构的串，从而确定子网络的结构。然后在训练集上训练子网络，在验证集上计算其精度值。以精度值作为反馈信号，采用策略梯度算法更新控制器网络的参数。在迭代时，控制器会以给予那些有更高精度值的神经网络以更高的概率值，从而确保策略函数能够输出最优网络结构。这一过程如下图所示。

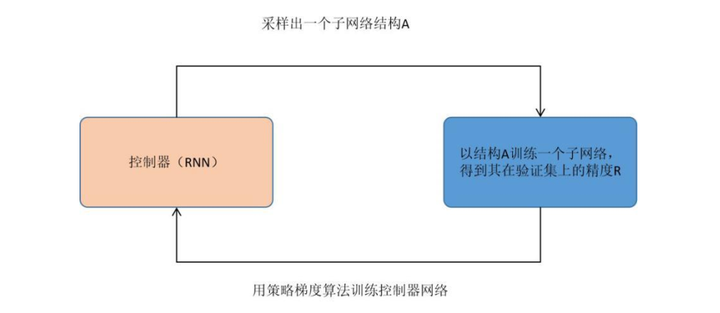
​ 算法的输出限定为分层的网络结构，第n个网络层以第n-1个网络层为基础。网络结构生成可抽象为序列生成问题，按层逐次预测网络结构。在RNN中，每5个输出值定义一个神经网络层。上一时刻的输出是本时刻的输入，确保RNN基于前面n-1层所有的结构信息来预测第n层的结构。RNN的输出层是softmax回归，根据它确定结构参数。对于卷积核高度，可以限定输出值为[ 1,3,5,7]四个数，RNN的softmax输出是取这4个数的概率值。

​ 控制器每一时刻的输出包括：卷积核的数量，卷积核的高度，卷积核的宽度，卷积操作在水平方向的步长，卷积操作在垂直方向的步长。这一过程如下图所示

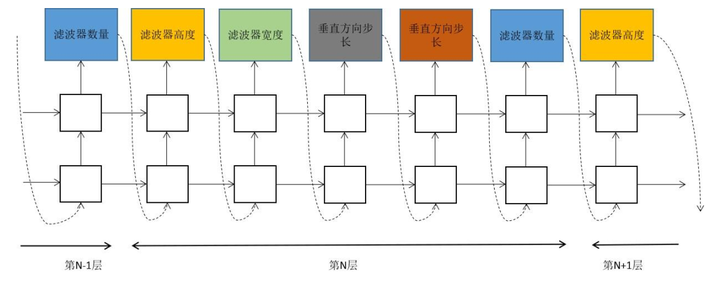
​ 实现时考虑典型的网络结构。对于卷积核的数量，取值范围为[ 24,36,48,64]，卷积核的高度取值范围为[ 1,3,5,7]，卷积核宽度的取值范围与高度相同。卷积步长可以固定为1，也可以按照 [ 1,2,3]取值。

​ 这里需要考虑的一个问题是何时终止预测，实现时限定了神经网络的层数，达到一定的层之后，停止输出。在训练过程中这个值会逐步增加。

​ 控制器生成该描述串之后，接下来在训练集上训练该子网络，这里采用了REINFORCE算法。目标函数为子网络在验证集上的精度的数学期望

其中 是控制器的参数， 是子网络， 是控制器输出的子网络所服从的概率分布， 是子网络在验证集上的精度值。直观的目标是某种结构的子网络准确率越高，则控制器生成该网络结构的概率越大。因此可以按照下式计算控制器的参数

其中R为子网络的准确率，p为生成该子网络结构的概率。实现时使用采样来近似数学期望值

其中m为mini-batch的样本数，T为神经网络的层数。为了解决REINFORCE算法计算出的梯度值偏差问题，在计算梯度时减掉了均值b

其中b为所有奖励的均值。前面介绍的方法只能生成标准的线性结构网络，通过改进可以生成跨层连接的卷积神经网络以及循环神经网络，通过在控制器softmax输出中增加相关信息而实现。

​ 文献[2]奠定了用强化学习解决NAS问题的基础，但面临计算量大的问题。一种解决方案是对搜索空间进行简化，限定网络结构为某些类型。回顾卷积网络的发展历史，各种典型卷积神经网络一般都具有某些重复、规整的结构，如ResNet中的跨层连接块，GoogLeNet中的Inception块等。如果能预测出这种基本块结构，然后将其堆叠形成网络，既可以降低搜索成本，又能使得网络随着输入数据的尺寸动态扩展，对于大尺寸的输入图像，只需要增加堆叠的块数即可。

​ 文献[3]采用了这种思想，提出了一种称为NASNet的方法。NASNet预测出基本块（building block），在小规模的CIFAR-10数据集上训练，然后将学习得到的网络结构迁移到更大规模的ImageNet数据集上。控制器预测的是基本两种网络单元，分别称为普通单元（Normal Cell）和约简单元（Reduction Cell）。前者不改变输入图像的尺寸，后者将图像的高度和宽度减半。根据这种设计，搜索整个神经网络结构的任务被简化为搜索最优基本块结构。除了降低搜索空间的大小，这种做法还使得在一个数据集上搜索得到的网络结构更容易泛化到其他数据集上。

​ 完整的神经网络通过这些相同结构的基本单元堆叠形成，但各个基本单元有不同的权重参数。对于不同尺寸和规模的数据集，使用了不同数量的基本块。下图为用于CIFAR-10和ImageNet数据集的网络结构。

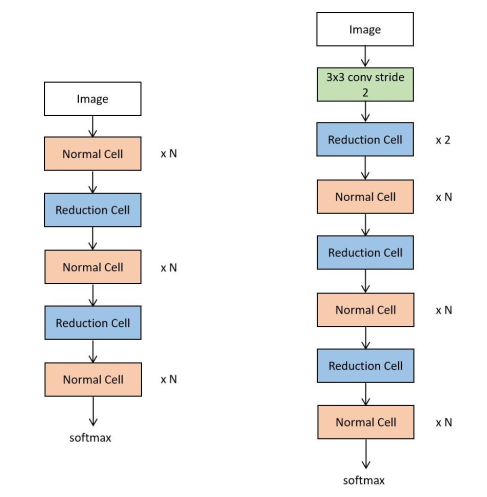
​ 上图中的乘以N表示这种基本块堆叠N次。算法的核心是如何生成基本块。控制器网络用RNN实现，其输出层为softmax，用于生成描述神经网络结构的决策。每个基本单元由B个块构成，每个块有两个输入，执行某一运算后产生输出。下图为生成每个块的方法，包含5个步骤：

• 选择一个隐含状态作为第一个输入
• 选择一个隐含状态作为第二个输入
• 为第一个隐含状态选择一个运算
• 为第二个隐含状态选择一个运算
• 为两个运算的结果选择一个合并方式，执行合并

隐含状态即神经网络前面的层的输出结果，如CNN中的卷积特征图像，或RNN中的隐含状态。然后对两个输入各选择一个运算，再将两个运算的结果合并。这一过程如下图所示。

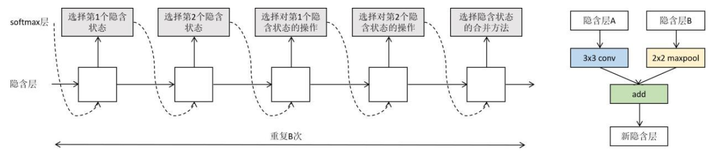
作用于隐含状态上的运算包括各种卷积，池化等操作。运算结果的合并方式有相加，拼接两种选择。

下图为生成一个基本单元的过程。图中上方为候选隐含状态集合，第1次选择H1和H2作为输入，分别执行池化和卷积运算，然后相加，得到H3，并将其加入候选隐含状态集合。接下来生成第2个块，选择H2和H3作为输入，分布执行卷积和恒等运算，将结果进行拼接，产生H4。其他的以此类推。在这里B的值由人工设定。

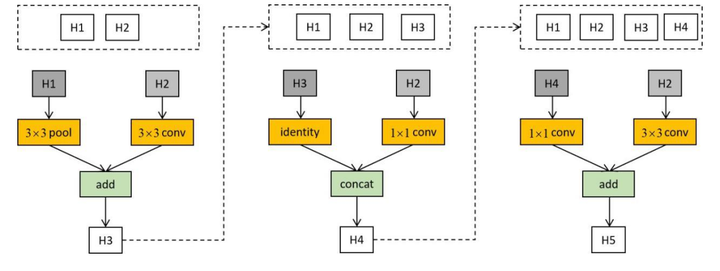
下图是典型的约简块，同样的B=4，这里将4个临时结果拼接，形成 作为本单元的输出值。

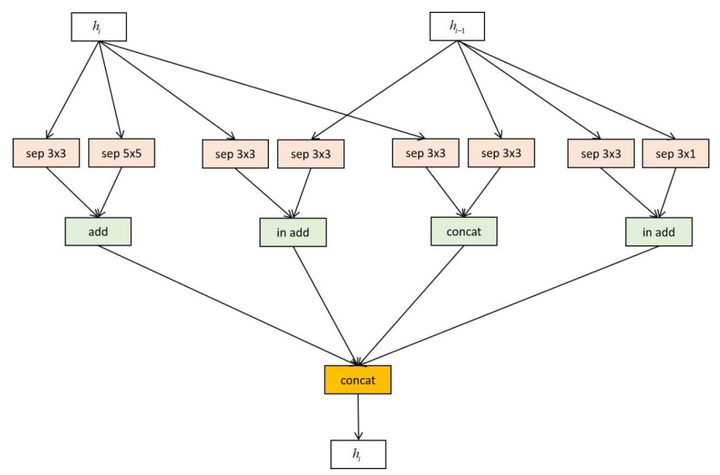
​ 在生成网络结构描述之后，训练子网络和控制器网络的方法与文献[2]相同，不同的是策略梯度算法采用了PPO算法（Proximal Policy Optimization）。

​ NASNet虽然在速度上有提升，但计算量还是太大。作为这一系列方法的改进，文献[4]提出了一种称为ENAS（Efficient Neural Architecture Search）的算法，通过在各个网络之间共享权重来减少计算量。由于各个子网络共享权重，因此每个子网络不需要从头开始训练，这极大的提高了搜索速度。

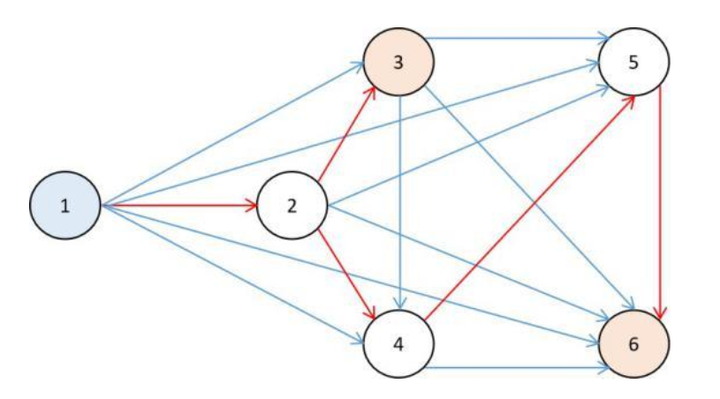
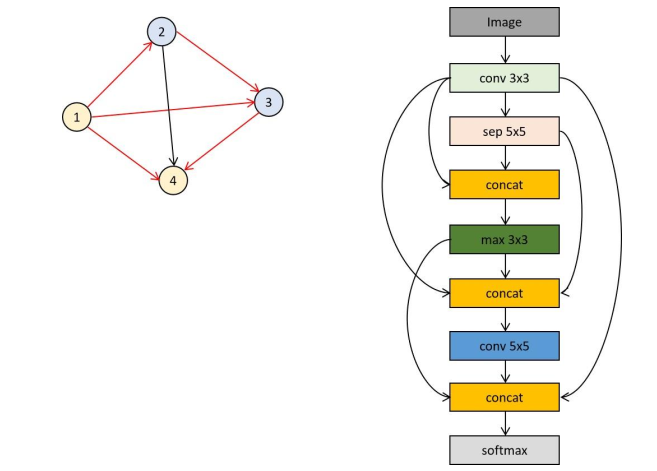
​ ENAS将NAS看做是寻找最优子图的问题，问题的解是一张大的图的子图。图23-1展示了这一概念。在这种图表示中，图的顶点为某种计算（如卷积，池化，相加），边表示数据的流动。下图的图有6个顶点，任意两个节点之间都可能有边连接，但边的方向只能是从编号较小的节点指向编号较大的节点，以防止环的出现。各个顶点可以对应于神经网络中的层，数据只能从编号小的层流向编号大的层。这个图的最优子图包含全部6个顶点，边为图中红色的边。

​ 使用这种表示，可以将NAS限定为在一个固定顶点数的图中寻找最优子图。神经网络的结构描述同样由RNN实现的控制器生成。对于卷积神经网络和循环神经网络采用了不同的描述，控制器生成这两种神经网络单元的方法也不同，下面分别介绍。

​ 循环神经网络中可以选择的操作为激活函数，包括ReLU和tanh两种类型。下图为一个子图以及对应的循环神经网络。

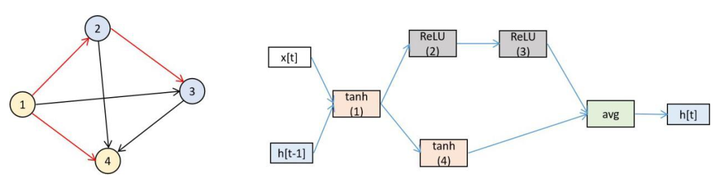
该图有4个顶点，红色的边表示信息的流动，黑色的边无效即没有使用。右图为对应的循环神经网络单元，运算节点的编号与左图中图的顶点编号对应。节点1接收 和 作为输入，执行下面的运算

这里的激活函数选用tanh，权重矩阵为本节点的参数。节点2以节点1的输出值为输入，选择ReLU作为激活函数，执行下面的运算

该节点同样有权重矩阵。节点3以节点2的输出值为输入，选择ReLU作为激活函数，执行下面的运算

节点4以节点1的输出值作为输入，选择tanh作为激活函数，执行下面运算

节点3和4没有后续节点，因此根据它们计算输出值。输出值为它们的均值

对每个 的节点对，都有一个独立的权重矩阵 ，为每个节点l一旦确定其前驱节点j，则使用该矩阵。在ENAS中，所有循环单元共用一组相同的权重参数。

​ 下面介绍控制器如何生成该网络结构。控制器在每次预测时需要做两个决策：确定以哪个节点的输出值作为输入即作为当前节点的前驱，为当前节点选用哪种激活函数。对于第1个节点，输入值是确定的，为 和 ，控制器只用为其选择激活函数。接下来生成节点2，首先选择一个节点作为输入即作为节点2的前驱节点，然后为节点2选择激活函数。其他节点依次类推，这一过程如下图所示。

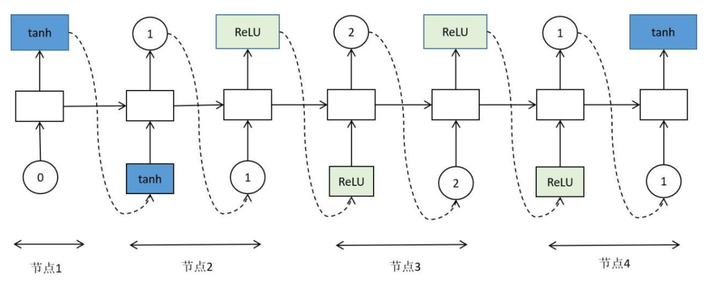
​ 假设循环神经网络的单元有N个节点，在生成第i个节点时，可以选择的前驱节点为[0,i-1]之间的整数，有i种情况，因此网络的拓扑结构有N!种。对于每种网络拓扑，每个节点的激活函数有4种选择，分别为tanh，sigmoid，identity，ReLU。因此可以搜索的网络结构总共有 种情况。

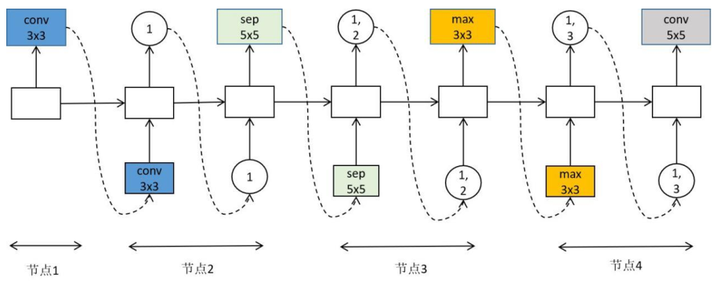
​ 下面介绍卷积神经网络的生成方式。下图给4个节点的卷积神经网络，同样的，红色的边表示有效边，黑色的未激活。这个图对应的网络结构如右图所示。

	与循环神经网络不同的是，**这里每个节点可以允许有多个前驱节点**。例如节点3有两个前驱，分别为1和2。

​ 生成卷积神经网络结构的方法与循环神经网络类似：为当前节点选择前驱节点，为当前节点选择要使用的运算。这两个决策结果形成卷积神经网络的一个层。这一过程如上图所示。

​ 对于第k层，小于等于k-1的不同层都可以用来作为它的输入，因此有 种连接关系。对于上图中的卷积神经网络，在k=4时选择{1,3}作为它的前驱，导致第1、3个层都与第4个层连接。这种做法可以形成任意的跨层连接。

​ 在每个节点处允许的运算有6种情况，分别是： 卷积， 卷积， 深度可分离卷积， 深度可分离卷积， 均值池化， 最大值池化。与循环神经网络相同，每个节点处都有所有运算的参数，并被所有网络结构共享。生成卷积神经网络结构的过程如下图所示。

如果一个卷积神经网络有L个层，则在第k层处有 种连接关系，由于各个层之间的连接关系是单独确定即相互独立的，因此网络的连接关系及拓扑结构有

种情况，对于每种网络结构，在每个层有6种可供选择的运算，因此所有可能的网络结构有

种情况。如果L=12，则所有可能的网络结构数为 。

​ 除了生成整个卷积网络，还可以生成卷积网络额单元然后将其堆叠形成完整的网络，具体做法与NASNet类似，不再重复介绍。

​ 生成网络结构之后，接下来的核心任务是训练子网络和控制器网络。假设控制器网络的参数为 ，子网络的参数为W，后者被所有子网络共享。这两组参数交替训练，在每次迭代时分两个阶段，首先训练W，然后训练 。

​ 第一阶段先固定住控制器的参数，控制器的输出策略为 ，从中采样出网络结构。以交叉熵作为损失函数，计算损失函数对w的梯度并更新。第二阶段固定住w，用 REINFORCE算法更新控制器的参数 ，最大化奖励值的数学期望

奖励值 为子网络m在验证集上的精度值。训练完成之后，根据控制器的策略 采样出多个子网络并训练，计算它们在验证集上的表现，选择表现最好的网络作为最终生成的网络。

​ 除上述方法之外，用强化学习实现NAS还有其他方案，具体可以阅读参考文献[11-13]。

性能评估策略

​ 对于搜索策略搜索出的神经网络结构，首先在一个训练集上训练，然后在验证集上测试精度值。训练和验证过程非常耗时，因此有必要采取措施以降低性能评估的成本。降低训练成本的简单做法有减少训练时间（迭代次数），在训练样本的一个子集上进行训练，在低分辨率的图像上进行训练，或者在训练时减少某些层的卷积核的数量。这些做法在降低计算成本的同时可能会导致性能评估值的偏差。虽然搜索策略只需对各种网络结构的优劣进行排序，无需知道它们准确的性能指标，但这种近似可能还是会导致排序结果的偏差。

​ 更复杂的做法是对神经网络的性能进行预测（外推），即通过训练时前面若干次迭代时的性能表现推断其最终的性能，或者用搜索出的单元（块）的特性预测整个网络的性能。权值共享也是一种方案。以之前训练过的子网络的权重作为当前要评估的子网络的初始权重可以有效的提高训练速度，加速收敛，避免从头开始训练。ENAS和DARTS则直接让各个子网络共享同一套权重参数。