损失函数

每个训练样本的平方误差损失（也称为L2 Loss）是实际值和预测值之差的平方

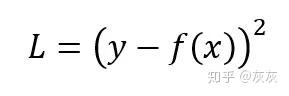
相应的成本函数是这些平方误差的平均值（MSE），它是一个二次函数（形式为ax^2+bx+c），并且值大于等于0,。二次函数具有全局最小值，由于没有局部最小值，所以永远不会陷入它。因此，可以保证梯度下降将收敛到全局最小值（如果完全收敛的话）

MSE损失函数通过使用平方误差来惩罚模型，有一个缺点，把一个比较大的数的平方会使它变得更大。但有一点需要注意，这个属性使MSE成本函数对异常值的健壮性降低。因此，如果我们的数据容易出现许多的异常值，则不应该使用它

每个训练样本的绝对误差是预测值和实际值之间的距离，与符号无关。绝对误差也称为L1 Loss

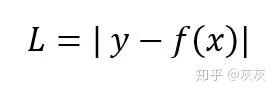
成本是这些绝对误差的平均值（MAE）。与MSE相比，MAE成本对异常值更加健壮。但是，在数学方程中处理绝对或模数运算符并不容易。

结合了MSE和MAE的最佳特性。对于较小的误差，他是二次的，否则是线性的（对于其梯度也是如此）。Huber损失需要确定 $\delta$ 参数

Huber损失对于异常值比MSE更强。它用于稳健回归，M估计法（M-estimator）和可加模型（additive model）。Huber损失的变体也可用于分类。

给分类基于应用于输入特征向量的规则则

熵是用来表示无序性和不确定性。测量具有芥蓝菜分布 $P(X)$ 的随机变量X

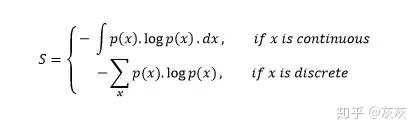
负号使用于最后结果为正数

概率分布的熵值越大，表明分布的不确定性越大。同样，一个较小的值代表一个更确定的分布

这使得二元交叉熵适合作为损失函数（你希望最小化其值）。我们对输出概率p的分类模型使用二元交叉熵损失

元素属于第1类（或正类）的概率=p

元素属于第0类（或负类）的概率=1-p

然后，输出标签y（可以取值0和1）的交叉熵损失和预测概率p定义为：

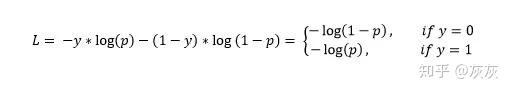
这也称为Log-Loss（对数损失）。为了计算概率p，可以使用sigmoid函数。其中，z是输入功能的函数

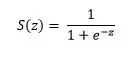
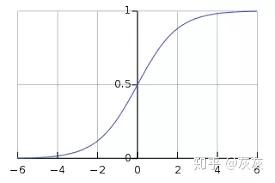
sigmoid函数的范围是[0, 1]这使得它适合于计算概率

Hinge损失主要用于带有类标签-1和1的支持向量机（SVM）。因此，请确保将数据集中“恶性”类标签从0更改为-1

Hinge损失不仅会惩罚错误的预测，还会惩罚不自信的正确预测

数据对(x, y)的Hinge损失如图：

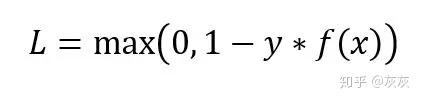
Hinge损失简化了SVM的数学运算，同时最大化了损失（与对数损失（Log-Loss）相比）。当我们想要做实时决策而不是高度关注准确性时，就可以使用它

多分类交叉熵损失是二元交叉熵损失的退矿。输入向量 $X_i$ 和相应的ont-hot编码目标向量 $Y_i$ 的损失是：

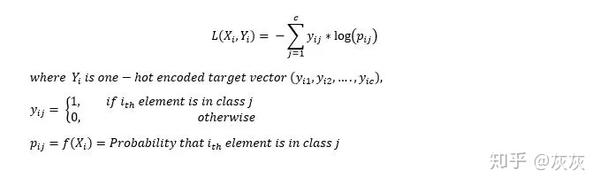
使用softmax函数来找到概率 $P_{ij}$

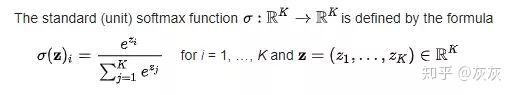
softmax层是接在神经网络的输出层前。Softmax层必须与输出层具有相同数量的节点

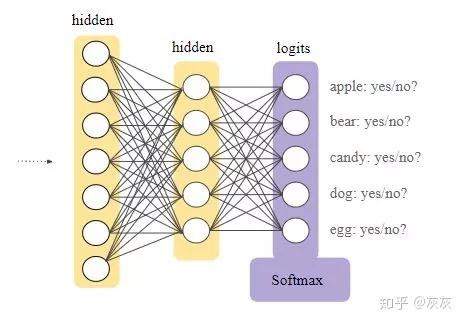
最后，我们的输出是具有给定输入的最大概率的类别

KL散度是概率分布与另一个概率分布区别的度量。KL散度为零表示分布相同

注意，发散函数不对称

与多分类分类相比，KL散度更常用于逼近复杂函数。我们在使用变分自动编码器（VAE）等深度生成模型时经常使用KL散度

损失函数的基本用法

1 2	criterion = LossCriterion() # 构造函数有自己的参数 loss = criterion(x, y) # 调用标准时也有参数

得到的loss结果已经对mini-batch数量取了平均值