Celery's Blog

0%

cGAN

发表于 更新于 Valine：

cGAN

为什么要有cGAN？

首先，GAN虽然厉害，但有个问题，其生成模型生成的样本完全是随机的，也就是完全取决于输入的噪声z，根本无法预测会生成数字1还是数字2.因此偶人提出了条件GAN，其思想也很简单，就是想要生成哪个数字，你输入的时候告诉我你想要的标签即可。为了达到这个目标，在训练的时候，就要加上标签。也就是G想要伪造数字1，就要在原本的z向量后面加十维的one-hot向量，在D那里也是，要判别什么，也要在尾部加上十维的one-hot向量

img

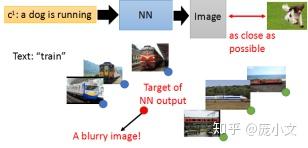
以上图为例，如果迷行的输入是文字，输出是图片，使用传统的做法会产生模糊的问题。比如输入火车，希望得到一张火车的图片，可是火车有侧面，有不同的形态，如果不加约束，则可能产生一张包含各种样式的火车的平均（模糊）图。

​ GAN的机制是只要识别器能分辨得出一张图是人工生成的还是原图就行，所以不能确保输入火车就回生成火车图片，比如输入火车生成一张很逼真的猫图，生成器也会被认为是一个成功的生成器（GAN容易钻空子，即如果某种特定形式可以骗过生成器，生成器会倾向于生成这种模式）

生成器输出一张图片，然后将同样的语句（条件）和生成的图片一起输入识别器，关键是，识别器不仅需要分辨真假，还需要分辨出语句（条件）和图片是否匹配。总的来说有三种情况：

原图 + 图和条件匹配 ----> 高分

原图 + 图和条件不匹配 ----> 低分

人工图 ----> 低分

img

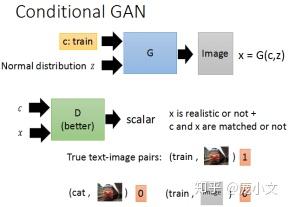
通过这样的操作，可以确保输出样本和条件是匹配的

CGAN有两种比较常用的结构：

img

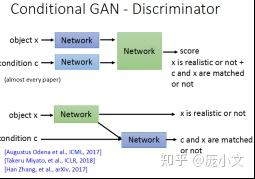
这两种结构的主要区别在生成器的输出部分，下面的可能更加合理：

下半部分的结构中生成器的输出分为两部分：

  • 是否是真实图片
  • 输出与条件是否匹配

这样做的好处是，直观上说，模型能分别知道两个任务的性能，更有针对性地提高模型能力，如果输出的图像不够真实，但是能比较好地是辈出是否匹配，则主要调节生成样本的分支，而第一种结构由于是混合在一起的，就没有这种针对性调节的能力。

值得一提的是，论文里的识别器使用了Patch的方法，即先将输出样本划分为若干个Patch，然后对每个Patch进行评分，最后将所有patch的得分平均作为最后得分。这样做的好处是，识别器能更加关注到生成图像的细节部分，即对高频的部分更加敏感，当然，最极端是每一个像素就是一个patch，这样的话识别器会失去大局观，即失去不同部分空间部分之间的相关信息

img

一些用到的函数的详解：

torch.nn.Embedding(num_embeddings, emcedding_dim, padding_idx = None, max_norm = None, norm_type = 2, scale_grad_by_freq = False, sparse = False)

1
2
3
4
5
6
7
8
9
# Pytorch官网的解释是：一个保存了固定字典的带下和简单查找表。这个模块常用来保存字典嵌入和用下标检索它们。模块的输入是一个下标的列表，输出是对应的词嵌入
# 个人理解：这是一个矩阵类，里面初始化了一个随机矩阵，矩阵的长是字典的大小，宽是用来表示字典中每个元素的属性向量，向量的维度根据你想要的元素的复杂度而定。类实例化之后可以根据字典中元素的下标来查找元素对应的向量。例如输入下标0， 输出就是embeds矩阵中的第0行
>>> import torch
>>> import torch.nn as nn
>>> from torch.autograd import Variable
>>> label = nn.Embedding(10, 10)
>>> label(Variable(torch.LongTensor([4])))
tensor([[-0.6134,  0.0528,  2.4490, -0.0294,  1.2371,  0.5792, -1.2843,  0.6881,
         -0.9275,  1.2503]], grad_fn=<EmbeddingBackward>)

nn.prod() 连乘函数

torch.cat() 连接函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
>>> x = torch.randn(2, 3)
>>> y = torch.randn(2, 3)
>>> x
tensor([[ 2.2045,  1.0283,  0.7637],
        [ 0.8578, -0.8376, -0.3780]])
>>> y
tensor([[-0.5941, -0.8588,  0.9540],
        [-1.1115,  0.3655,  0.2471]])
>>> torch.cat((x, y), 0)
tensor([[ 2.2045,  1.0283,  0.7637],
        [ 0.8578, -0.8376, -0.3780],
        [-0.5941, -0.8588,  0.9540],
        [-1.1115,  0.3655,  0.2471]])
>>> torch.cat((x, y), 1)
tensor([[ 2.2045,  1.0283,  0.7637, -0.5941, -0.8588,  0.9540],
        [ 0.8578, -0.8376, -0.3780, -1.1115,  0.3655,  0.2471]])
>>> torch.cat((x, y), -1)
tensor([[ 2.2045,  1.0283,  0.7637, -0.5941, -0.8588,  0.9540],
        [ 0.8578, -0.8376, -0.3780, -1.1115,  0.3655,  0.2471]])
# torch.cat((), 0)	竖着连接
# torch.cat((), 1 or -1)	横着连接

numpy.random.randint(low, high, size)

low、high、size三个参数。默认high是None，如果只有low，那范围就是[0, low)。如果有high，范围就是[low, high)

1
2
3
4
5
6
>>> a = np.random.randint(5, 16, 64)
>>> a
array([13, 14, 12, 15,  8, 13, 14, 11, 11, 10, 14, 15,  8, 15,  5, 12,  6,
       15,  9,  5,  5, 13, 13,  8, 15, 10, 11,  6,  8, 15,  9,  9,  9,  5,
       13, 12, 12,  8,  5, 14,  7, 15, 11,  6,  7, 12, 10,  8, 10,  5, 13,
        9, 14,  8,  7,  6,  7,  6,  6, 12, 13, 15, 14, 10])

np.random.normal(loc=0.0, scale=1.0, siez=None)

loc：float，此概率分布的均值（对应整个分布的重心center）

scale：float，此概率分布的标准差（对应于分布的宽度，scale越大越矮胖。scale越小，越瘦高）

size：int or tuple of ints

输出的shape，默认为None， 值输出一个值

1
2
3
4
5
6
7
>>> a = np.random.normal(5, 1)
>>> a
4.687275350809846
>>> a = np.random.normal(5, 1, [2, 2])
>>> a
array([[5.18009118, 4.91448971],
       [6.2771917 , 5.15529855]])

IS(G)=exp(Ex∼pgDKL(p(y∣x)∣∣p(y)))IS(G) = exp(E_{x \sim p_g}D_{KL}(p(y|x)||p(y)))

$D(p||q) = \sum p(x) log \frac{p(x)} {q(x)} $

FID=∣∣ur−ug∣∣2+Tr(∑r+∑g−2(∑r−∑g)12)FID = ||u_r - u_g||^2 + T_r(\sum_r + \sum_g - 2(\sum_r - \sum_g)^{\frac{1} {2}})