StyleGAN

**原有GAN出现的问题：**与多数GAN一样，proGAN控制生成图像的特定特征的能力非常有限。这些属性相互纠缠，即使略微调整输入，也会同时影响生成图像的多个属性。所以如何将ProGAN该位条件生成模型，或者增强其微调单个属性的能力，是一个可以研究的方向。

解决的方法：

StyleGAN是NVIDIA继ProGAN之后提出的新的生成网络，其主要通过修改每一层级的输入，在不影响其它层级的情况下，开控制该层级所表示的视觉特征。这些特征可以使粗的特征（如姿势、脸型等），也可以是一些细节特征（如瞳色、发色等）

本文的工作及贡献：

• 借鉴风格迁移，提出基于样式的生成器（style-based generator）

  • 实现了无监督地分离高级属性（人脸姿势、身份）和随机变化（例如雀斑，头发）
  • 实现对生成图像中特定尺度的属性的控制
  • 生成器从一个科学系的常量输入开始，隐码在每个卷积层调整图像的“样式”，从而直接控制不同尺度下图像特征的强度。

• 实现了对**隐空间（latent space）**较好的解耦

  • 生成器将输入的隐码z嵌入一个中间的隐空间。因为输入的隐空间Z必须服从训练数据的概率密度，这在一定程度上导致了不可避免的纠缠，而嵌入的中间的隐空间W不受这个控制，因此可以被解耦

• 提出了两个新的量化隐空间解耦程度的方法

  • 感知路径长度和线性可分性。与传统的生成器相比，新的生成器允许更线性、更解耦地表示不同的变化因素

• 提出了新的高质量的人脸数据集（FFHQ,7万张1024 * 1024的人脸图片）

  

2. 模型和方法

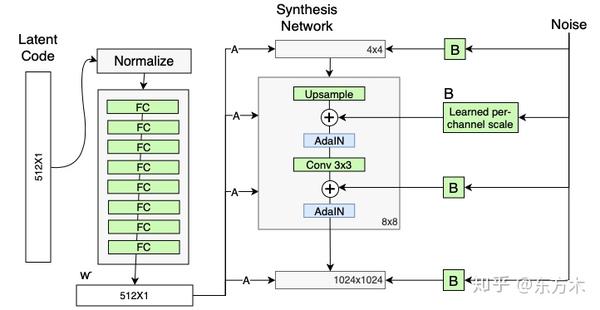
2.1 基于样式的生成器结构

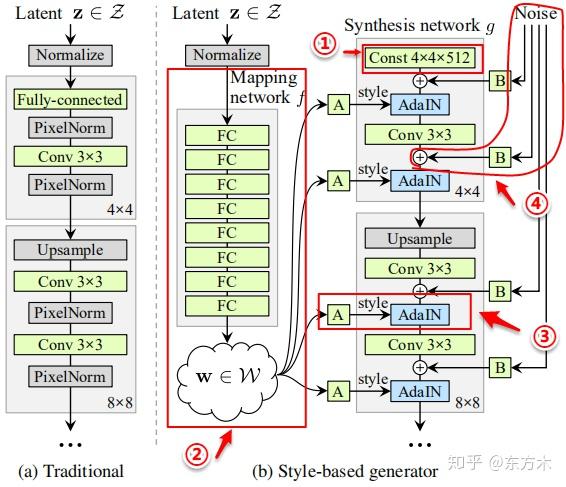
总共有18层，每个分辨率有两个卷积层（4， 8， 16， …1024）

• 1.移除了传统的输入

• 2.映射网络

• 3.样式模块（AdaIN，自适应实例归一化）

• 4.随机变化（通过加入噪声为生成器生成随机细节）

移除传统输入

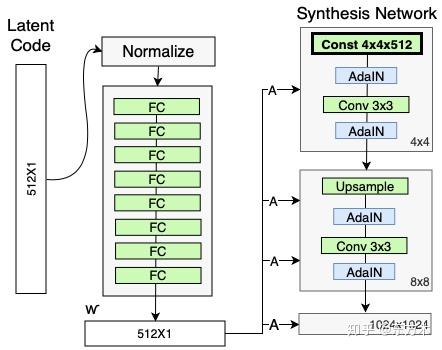
传统的生成器使用latent code（随机输入）作为生成器的初始输入；StyleGAN抛弃了这种设计，将一个可学习的常数作为生成器的初始输入。一个假设是它减少了特征纠缠——对于网络来说，只使用w而不依赖纠缠的输入向量更容易学习

映射网络（Mapping Network）

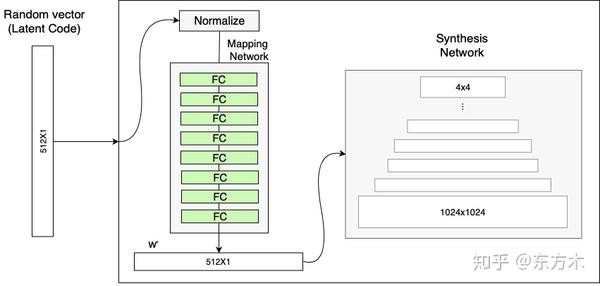
映射网络由8个全连接层组成，其输出w与输入z大小相同（512 * 1）。映射网络的目标是将输入向量编码为中间向量，中间向量W的不同元素控制不同的视觉特征。

使用输入向量z控制视觉特征的能力是有限的，它必须遵循训练数据的概率密度。例如，如果黑色头发的人的图像在数据集中更加常见，那么更多的输入值将映射到该特性。因此该模型无法将输入向量z的一部分（向量中的元素）映射到特征，这种向量称为特征纠缠。

但是，通过映射网络，该模型可以生成一个不需要跟随训练数据分布的向量w，并且可以减少特征之间的相关性（解耦，特征分离）

样式模块（AdalN）

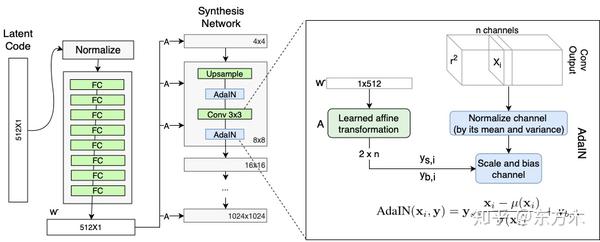
W通过每个卷积层的AdaIN输入到生成器的每一层中。

计算方法：

• 计算每个特征图xi（feature map）独立进行归一化特征图中的每个值减去该特征值的均值然后除以方差。
• 一个可学习的仿射变换（全连接层）将w转换为style中AdaIN的平移和缩放因子 $y = (y_s, i, y_b, i)$
• 然后对每个特征图分别使用style中学习到的平移和缩放因子进行尺度和平移变换

这里的不同之处在于这里的缩放和平移是用隐码w计算得到，而不是用一个图像计算得到的。

随机变化（通过引入噪声为生成器生成随机细节）

人的连有很多可以看做是随机的，比如头发的精确位置，使特向更真实，增加了输出的多样性。将这些小特征插入GAN图像的常用方法是向输入向量添加随机噪声，然后通过输入层输入生成器。然而，在很多情况下，控制噪声效果是很棘手的，因为特征纠缠现象，略微改变噪声会导致图像的其他特征收到影响。

该框架通过在合成网络的每个分辨率级上增加尺度化的噪声来回避这些问题。噪声是由高斯噪声组成的单通道图像，将一个噪声图像提供给合成网络的一个特征图。在卷积之后、AdaIN之前将高斯噪声加入生成器网络中。B使用可学习的缩放参数对输入的高斯噪声进行变换，然后将噪声广播到所有的特征图中（分别加到每个特征图上，每个特征图对应一个可学习的scale参数）

2.2 正则化-混合正则化（mixing regularization）

为了进一步距离styles的局部化（减少不同层之间样式的相关性），本文对生成器使用混合正则化。

方法：对给定的训练样本（随机选取）使用样式混合的方式生成图像。在训练过程中，使用两个随机隐码z（latent code）而不是一个，生成图像时，在合成网络中随机选择一个点（某层），从一个隐码切换到另一个隐码（称之为样式混合）。具体来说，通过映射网络运行两个潜码z1、z2，并让对应的w1、w2控制样式，使w1在交点前应用，w2在交点后应用

这种正则化技术防止网络假设相邻样式是相关的，随机切换确保网络不会学习和依赖级别之间的相关性。

2.3 两种新的量化隐空间（latent space）耦合度的方法

• 解耦的目标是使隐空间（latent space）由线性子空间组成，即每个子空间（每个维度）控制一个变异因子（特征）

• 但是隐空间Z中的各个因子的采样概率需要与训练数据中响应的密度匹配，就会产生纠缠。而中间隐藏空间W不需要根据任何固定分布进行采样，他的采样密度是由可学习的映射网络f(z)得到的，使变化的因素变得更加线性。

• 本文假设，生成器基于解耦的表示比基于纠缠的表示应该更容易产生真实的图像（若在FID变小的同时，隐空间耦合度变小，则可以得证）。因此，我们期望训练在无监督的情况下（即，当不预先知道变异的因素时）产生较少纠缠的W

• **最近提出的用于量化解耦的指标，需要将一个输入图像映射到隐码的编码器网络。**但是不适合本文，因为baseline GAN缺乏这样的编码器

• 所以本文提出了两种新的量化解耦的方法，他们都不需要编码器，所以对于任何数据集和生成器都是可计算的

  • 感知路径长度（Perceptual path length）
  • 线性可分性（Linear separability）

感知路径长度

为什么这种量化纠缠的方法是可行的？

• 对隐空间向量进行插值会在图像中产生非线性变化。比如，在所有断点中缺失的特征可能会出现在线性插值路径的中间。这表明隐空间是耦合的，变化因子没有被恰当的分开。所以通过测量当在两个隐空间之间进行插值时图像的剧烈变化程度，可以反映隐空间的纠缠程度（特征分离程度）

感知路径长度计算，使用10000个样本计算

• 将两个隐空间之间的插值路径细分为小段，感知总长度定义为每段感知差异的总和。感知路径长度的定义是这个和在无限细的细分下的极限，实际上是用一个小的细分来近似它。隐空间Z中所有可能端点（在路径中的位置）的平均感知路径长度，计算如下：
• 其中。t服从0， 1分布，slerp表示球面插值操作，这是在归一化的输入隐空间中最合适的插值方式。
• G是生成器，d计算得到生成图像之间的感知距离。因为d是二次的，所以除以而不是来消除对细分粒度的依赖
• d的具体计算方式：使用基于感知的成对距离图像，测量连续图像之间的差异（两个VGG16 embeddings之间的差异，利用VGG16提取出图像的特征，在特征层面上计算距离）

计算隐空间W的感知路径的长度与z的唯一不同时采用lerp线性插值，因为w向量没有进行归一化

线性可分性（linear separability）

为什么这种量化纠缠的方法是可行的？

**如果一个隐空间是充分解耦的，应该能够找到与每个变化因子对应的方向向量。**我们提出了另一种度量方法来量化这种效果，测量通过线性超平面将隐空间点分割成两个不同集合的程度，使每个集合对应于图像的特定的二元属性（比如男、女）

计算方法：

• 训练40个辅助分类器，分别对40个二元属性进行区分（每个分类器区分一个属性）。分类器与StyleGAN判别器结构相同，使用CelebA-HQ数据集训练得到（保留原始CelebA的40个属性，150000个训练样本),学习率10-3，批次大小8，Adam优化器。
• 使用生成器生成的200,000个图像，并使用辅助分类器进行分类，根据分类器的置信度对样本进行排序，去掉置信度最低的一般，得到100,000个一直类别的隐空间向量（latent code）
• 对于每个属性，拟合一个线性SVM来预测标签——基于传统的隐空间点或基于样式的隐空间点w—并且根据这个超平面对这些隐空间点（512维，100,0000个点）进行分类
• 用条件熵H(Y |X)度量超平面将点划分为正确类别的能力，X是SVM预测的类别，Y是预先训练好的辅助分类器确定的类（作为真实类别）；因此，根据SVM确定样本在超平面的哪一边，条件熵告诉我们需要多少额外的信息来确定样本的真实类别。直觉上，如果隐空间中的变化因子是耦合的（非线性的），那么用超平面来分离样本点将会更加困难（需要更多的额外信息），产生高的条件熵。较低的值表示易于分离（可分性好），因此解耦程度更大

可分性计算公式 ，其中i列举了40个属性。取幂是为了将值从对数域变换为线性域，便于进行比较

截断技巧

考虑到训练数据的分布，低密度区域很少被表示，因此生成器很难学习该区域。通过对隐空间进行阶段可以提升生成影响的平均质量，虽然会损失一些变化。对中间隐码W进行阶段，迫使W接近平均值

经过试验：噪声只会影响随机方面，而保留了整体结构和身份、面部等高级特征。

$\epsilon$