Celery's Blog

0%

LeetCode-Day30

发表于 Valine：

LeetCode-Day30——栈

456. 132模式

给定一个整数序列：a1, a2, …, an，一个132模式的子序列 ai, aj, ak 被定义为：当 i < j < k 时，ai < ak < aj。设计一个算法，当给定有 n 个数字的序列时，验证这个序列中是否含有132模式的子序列。

注意：n 的值小于15000。

示例1:

1
2
3
输入: [1, 2, 3, 4]
输出: False
解释: 序列中不存在132模式的子序列。

示例 2:

1
2
3
输入: [3, 1, 4, 2]
输出: True
解释: 序列中有 1 个132模式的子序列： [1, 4, 2].

示例 3:

1
2
3
输入: [-1, 3, 2, 0]
输出: True
解释: 序列中有 3 个132模式的的子序列: [-1, 3, 2], [-1, 3, 0] 和 [-1, 2, 0].

思路：

这里主要是采取栈的思想。

从vector末尾开始遍历，栈顶存放的是当前的最大值，如果nums[j] > max.top()，（假设max.top()在vector中原始的下标是k），则现在已经满足了j < k && nums[j] > nums[k]，即已经满足了32 模式，此时，在往下找，如果i对应的nums[i]小于third，则算找到了i < j < k && nums[i] < nums[k] < nums[j]。

Code如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
public:
    bool find132pattern(vector<int>& nums) {
        if(nums.size() < 3) {
            return false;
        }
        stack<int> max;
        int third = INT_MIN;
        for(int i = nums.size() - 1;i >= 0;i--) {
            if(nums[i] < third)  {
                return true;
            }
            while(!max.empty() && nums[i] > max.top()) {
                third = max.top();
                max.pop();
            }
            max.push(nums[i]);
        }
        return false;
    }
};

496. 下一个更大元素I

给定两个没有重复元素的数组 nums1 和 nums2 ，其中nums1 是 nums2 的子集。找到 nums1 中每个元素在 nums2 中的下一个比其大的值。

nums1 中数字 x 的下一个更大元素是指 x 在 nums2 中对应位置的右边的第一个比 x 大的元素。如果不存在，对应位置输出-1。

示例 1:

1
2
3
4
5
6
输入: nums1 = [4,1,2], nums2 = [1,3,4,2].
输出: [-1,3,-1]
解释:
    对于num1中的数字4，你无法在第二个数组中找到下一个更大的数字，因此输出 -1。
    对于num1中的数字1，第二个数组中数字1右边的下一个较大数字是 3。
    对于num1中的数字2，第二个数组中没有下一个更大的数字，因此输出 -1。

示例 2:

1
2
3
4
5
输入: nums1 = [2,4], nums2 = [1,2,3,4].
输出: [3,-1]
解释:
    对于num1中的数字2，第二个数组中的下一个较大数字是3。
    对于num1中的数字4，第二个数组中没有下一个更大的数字，因此输出 -1。

注意:

nums1和nums2中所有元素是唯一的。
nums1和nums2 的数组大小都不超过1000。

递增栈（从栈顶到栈底增加）：

  • 元素入栈之后，其下面元素一定是其左边第一个比它大的数（可用来求每个元素左边更大的第一个元素）

  • 若在元素插入之前，栈顶元素比插入元素小，那么栈顶元素一定是插入元素左边第一个比它小的数

  • 若在元素插入之前，栈顶元素比插入元素小，那么待插入元素是所有需要出栈的元素右边第一个更大的元素（可用来求每个元素右边更大的第一个元素）

  • 最后一定会留下最大的数（对较大的数更有利）

递减栈也同理。

​ 所以，这道题就是这样一个递增栈，我们从vector末尾开始遍历容器，当前的元素比栈顶元素要大的时候，则应该不断的弹栈，直到遇到一个比当前元素更大的栈顶元素或者栈已经为空的时候，如果栈顶为空，则说明，该元素右边不存在比它大的元素，如果栈顶不为空，则说明，栈顶元素就是该元素右边第一个比它大的元素。

如果当前的元素小于栈顶元素，则直接入栈。（因为当前的栈顶元素就是当前元素右边第一个比他大的数字）

Code如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
vector<int> nextGreaterElement(vector<int>& nums1, vector<int>& nums2) {
    stack<int> st;
    map<int, int> PMap;
    vector<int> res;
    for(int i = nums2.size() - 1;i >= 0;i--) {
        if(st.empty()) {
            PMap.insert({nums2[i], -1});
        } else if(st.top() > nums2[i]) {
            PMap.insert({nums2[i], st.top()});
        } else {
            while(!st.empty() && st.top() < nums2[i]) {
                st.pop();
            }
            if(st.empty()) {
                PMap.insert({nums2[i], -1});
            } else {
                PMap.insert({nums2[i], st.top()});
            }
        }
        st.push(nums2[i]);
    }

    for(int i = 0;i < nums1.size();i++) {
        res.push_back(PMap[nums1[i]]);
    }
    return res;
}

503. 下一个更大元素II

给定一个循环数组（最后一个元素的下一个元素是数组的第一个元素），输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1。

示例 1:

1
2
3
4
5
6
输入: [1,2,1]
输出: [2,-1,2]
解释: 第一个 1 的下一个更大的数是 2；
数字 2 找不到下一个更大的数； 
第二个 1 的下一个最大的数需要循环搜索，结果也是 2。
注意: 输入数组的长度不会超过 10000。

思路：

下次遇到循环数组，可以多复制一遍原数组

方法一. 栈

依然还是采用栈的想法

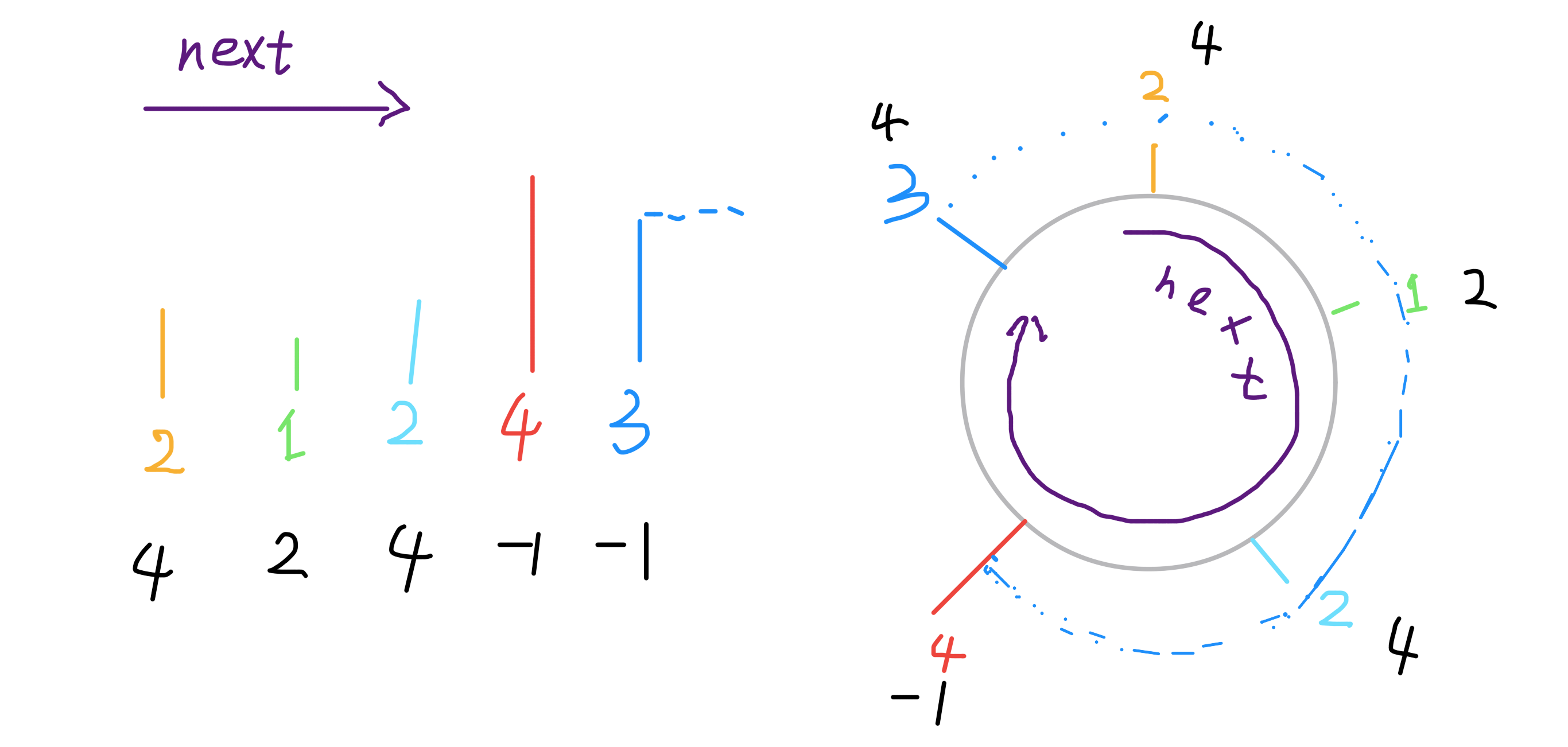
给你一个数组[2,1,2,4,3]，你返回数组[4,2,4,-1,4]。拥有了环形属性之后，最后一个元素3绕了一圈后找到了比自己大的元素4。

ink-image (1)

首先，计算机的内训都是线性的，没有真正意义上的换型数组，但是我们可以模拟出环形数组的效果，一般都是通过%运算求模（余数），获得环形特效：

回到这个问题，增加了环形属性之后，问题的难点在于：这个Next数组的意义不仅仅是当前元素的右边了，有可能出现在当前元素的左边（如上例）

我们可以考虑这样的思路：

将原始数组“翻倍”，就是在后面再接一个原始数组，这样的话，按照之前“比身高”的流程，每个元素不仅可以比较自己右边的元素，而且也可以和左边的元素比较了

ink-image (2)

如何实现？首先是将这个双倍数组构造出来，然后套用算法模板，但是我们可以不构造新数组，而是利用循环数组的技巧来模拟。

上Code:

1
2
3
4
5
6
7
8
9
10
11
12
13
vector<int> nextGreaterElements(vector<int>& nums) {
    int n = nums.size();
    vector<int> result;
    stack<int> s;
    for(int i = 2 * n - 1;i >= 0;i--) {
        while(!s.empty() && s.top() <= nums[i % n]) {
            s.pop();
        }
        res[i % n] = s.empty() ? -1 : s.top();
        s.push(nums[i % n]);
    }
    return result;
}

方法二.

就是我们在计算当前元素(nums[i])的下一个比他大的元素的时候，可以先看看nums[i + 1]是否比它大，如果nums[i + 1]比它大，则说明nums[i]下一个比它大的元素就是nums[i + 1]，若不是，就比较result[i + 1]，如果result[i + 1] > nums[i]，则说明比nums[i]大的下一个元素就是result[i + 1]，如果还不是，就接着往下比较result[i + 2]...如果已经到最后一个元素的话，就说明他右边已经没有元素比他大了，因此从左边开始遍历，寻找比他大的元素。

Code实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
vector<int> nextGreaterElements(vector<int>& nums) {
    int length = nums.size();
    vector<int> result(length, 0);
    for(int i = length - 1; i >= 0;i--) {
        int j = i + 1;
        for(;j < length;j++) {
            if(nums[i] < nums[j]) {
                result[i] = nums[j];
                break;
            } else if(nums[i] < result[j]) {
                result[i] = result[j];
                break;
            }
        }
        if(j == length) {
            for(j = 0;j < i;j++) {
                if(nums[j] > nums[i]) {
                    result[i] = nums[j];
                    break;
                }
            }
            if(j == i) {
                result[i] = -1;
            }
        }
    }   
    return result;     
}