LeetCode-Day29

LeetCode-Day29 贪心算法专题

贪心算法可以认为是动态规划算法的一个特例，相比动态规划，使用贪心算法需要满足更多的条件（贪心选择性质），但是效率比动态规划要高。

比如说一个算法问题使用暴力解法需要指数级时间，如果能使用动态规划消除重叠子问题，就可以降到多将是级别，如果满足贪心选择性质，那么可以进一步降低时间复杂度，达到线性级别的。

那么，什么是贪心选择性质呢？简单的说就是：每一步做出一个局部最优的选择，最终的结果就是全局最优。注意，这是一种特殊性质，其实只有一部分问题拥有这个性质。

402. 移掉k位数字

给定一个以字符串表示的非负整数 num，移除这个数中的 k 位数字，使得剩下的数字最小。

注意:

num 的长度小于 10002 且 ≥ k。
num 不会包含任何前导零。
示例 1 :

1
2
3

输入: num = "1432219", k = 3
输出: "1219"
解释: 移除掉三个数字 4, 3, 和 2 形成一个新的最小的数字 1219。

示例 2 :

1
2
3

输入: num = "10200", k = 1
输出: "200"
解释: 移掉首位的 1 剩下的数字为 200. 注意输出不能有任何前导零。

示例 3 :

1
2
3

输入: num = "10", k = 2
输出: "0"
解释: 从原数字移除所有的数字，剩余为空就是0。

思路：

利用栈，从首位开始，如果当前的数字比栈顶的数字要小，则把栈顶的数字弹出，直至栈顶数字小于当前的数字或者栈为空的时候，将该数字放入栈中。

当k位数字放完之后，考虑去除在栈中的首位数字为0的情况，最后返回栈中的字符串和余下未被删除的字符串的拼接。

Code：

class Solution {
public:
    string removeKdigits(string num, int k) {
        stack<char> word;
        word.push(num[0]);
        for (int i = 1; i < num.size(); i++)
        {
            while (!word.empty() && word.top() > num[i] && k > 0)
            {

                word.pop();
                k--;
            }
            word.push(num[i]);
        }
        for (int i = k; i > 0; i--)
        {
            word.pop();
        }
        string new_word = "";
        while (!word.empty())
        {
            new_word += word.top();
            word.pop();
        }
        for (int i = 0, j = new_word.size() - 1; i < j; i++, j--)
        {
            char temp = new_word[i];
            new_word[i] = new_word[j];
            new_word[j] = temp;
        }
        //去掉首位的０
        int index = 0;
        while (new_word[index] == '0')
        {
            index++;
        }
        if (index == new_word.size())
            return "0";
        return new_word.substr(index);
    }
};

406. 根据身高重建队列

假设有打乱顺序的一群人站成一个队列。每个人由一个整数对(h, k)表示，其中h是这个人的身高，k是排在这个人前面且身高大于或等于h的人数。编写一个算法来重建这个队列。

注意：
总人数少于1100人。

示例

输入:
[[7,0], [4,4], [7,1], [5,0], [6,1], [5,2]]

输出:
[[5,0], [7,0], [5,2], [6,1], [4,4], [7,1]]

思路：先排序后插入

假设候选队列为A，已经站好队的队列为B

从A里挑身高最高的人x出来，插入到B，因为B中每个人的身高都比x要高，因此x插入的位置，就是看x前面应该有多少人就行了。比如x前面有5个人，那x就插入到队列B的第5个位置。

vector<vector<int>> reconstructQueue(vector<vector<int>>& people) {
    sort(people.begin(), people.end(), [](const vector<int>& a, const vector<int>& b) {
        if(a[0] > b[0]) return true;
        if(a[0] == b[0] && a[1] < b[1]) return true;
        return false;
    });
    vector<vector<int>> res;
    for(auto& e: people) {
        res.insert(res.begin() + e[1], e);
    }
    return res;
}

452. 用最少数量的箭引爆气球

在二维空间中有许多球形的气球。对于每个气球，提供的输入是水平方向上，气球直径的开始和结束坐标。由于它是水平的，所以y坐标并不重要，因此只要知道开始和结束的x坐标就足够了。开始坐标总是小于结束坐标。平面内最多存在104个气球。

一支弓箭可以沿着x轴从不同点完全垂直地射出。在坐标x处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend，且满足 xstart ≤ x ≤ xend，则该气球会被引爆。可以射出的弓箭的数量没有限制。弓箭一旦被射出之后，可以无限地前进。我们想找到使得所有气球全部被引爆，所需的弓箭的最小数量。

Example:

输入:
[[10,16], [2,8], [1,6], [7,12]]

输出:
2

解释:
对于该样例，我们可以在x = 6（射爆[2,8],[1,6]两个气球）和 x = 11（射爆另外两个气球）。

思路：

首先，想到的就是先排序，按照points的first从小到大，second从大到小，然后，不断缩小范围直至范围不存在，则需要箭的数量+1

Code如下：

class Solution {
public:
    int findMinArrowShots(vector<vector<int>>& points) {
        if(points.size() <= 1) {
            return points.size();
        }
        sort(points.begin(), points.end(), [](const vector<int>& a, const vector<int>& b) {
            if(a[0] < b[0]) return true;
            if(a[0] == b[0] && a[1] > b[1]) return true;
            return false;
        });
        int count = 1;
        int left = points[0][0], right = points[0][1];
        for(int i = 1;i < points.size();i++) {
            left = max(left, points[i][0]);
            right = min(right, points[i][1]);
            if(left > right) {
                count++;
                left = points[i][0];
                right = points[i][1];
            }
        }
        return count;
    }
};

435. 无重叠区间

问题概述：这是一个很经典的贪心算法问题Interval Scheduling（区间调度问题）。给你很多形如[start, end]的闭区间，请你设计一个算法，算出这些区间中最多有几个互不相交的区间。

这个问题，在生活中应用广泛，比如你今天有好几个活动，每个活动都可以用区间[start, end]表示开始和结束的时间，请问你今天最多能参加几个活动呢？显然你一个人不能同时参加两个活动，所以说这个问题就是求这些时间区间的最大不相交子集。

贪心解法：

这个问题可以分为以下三个步骤：

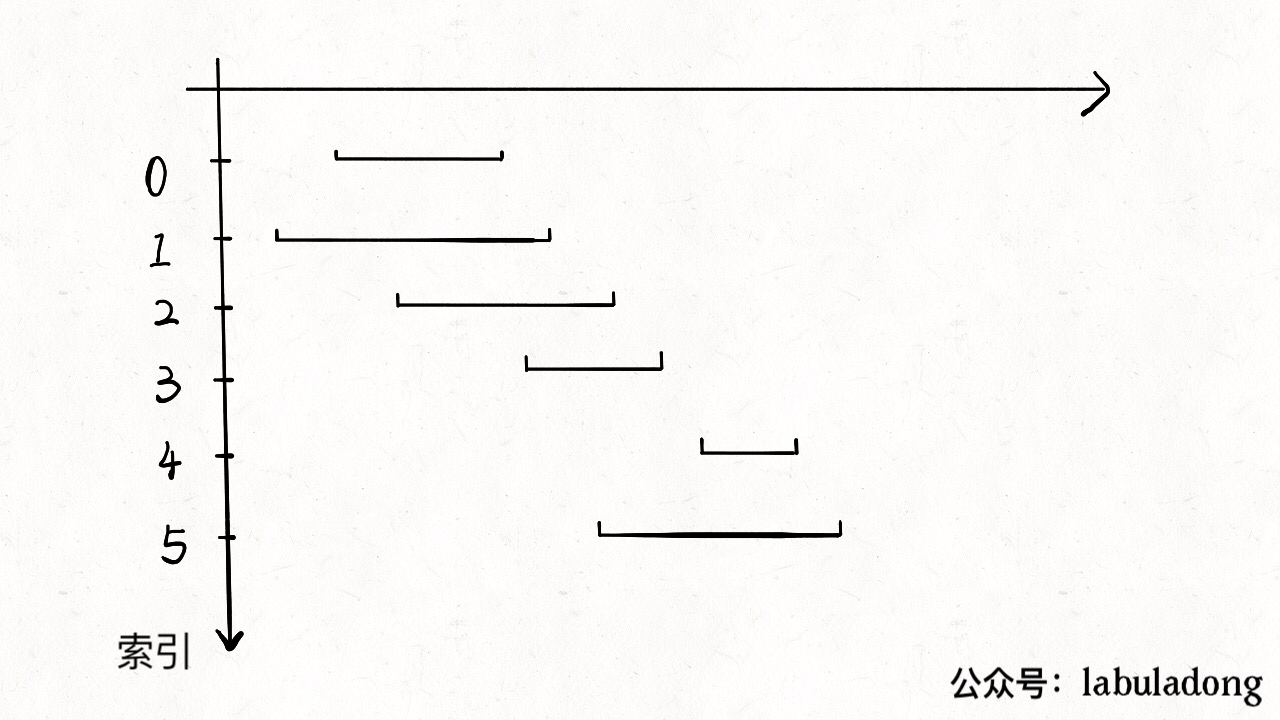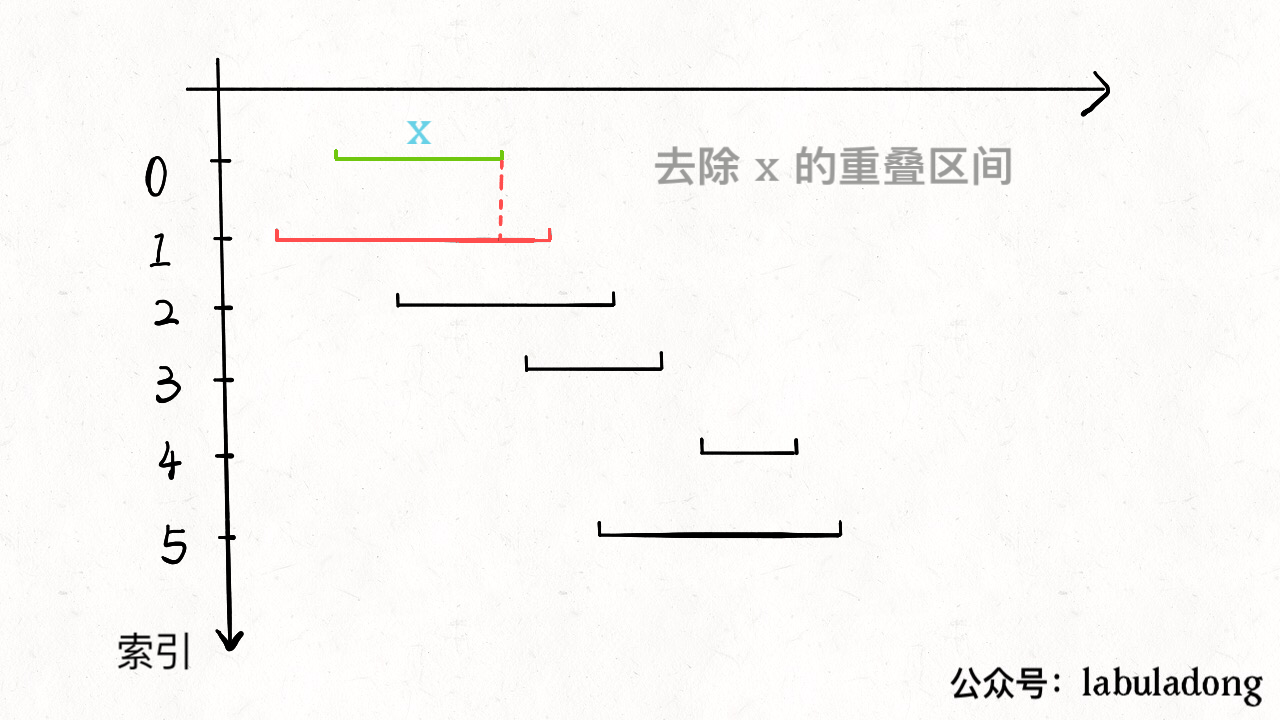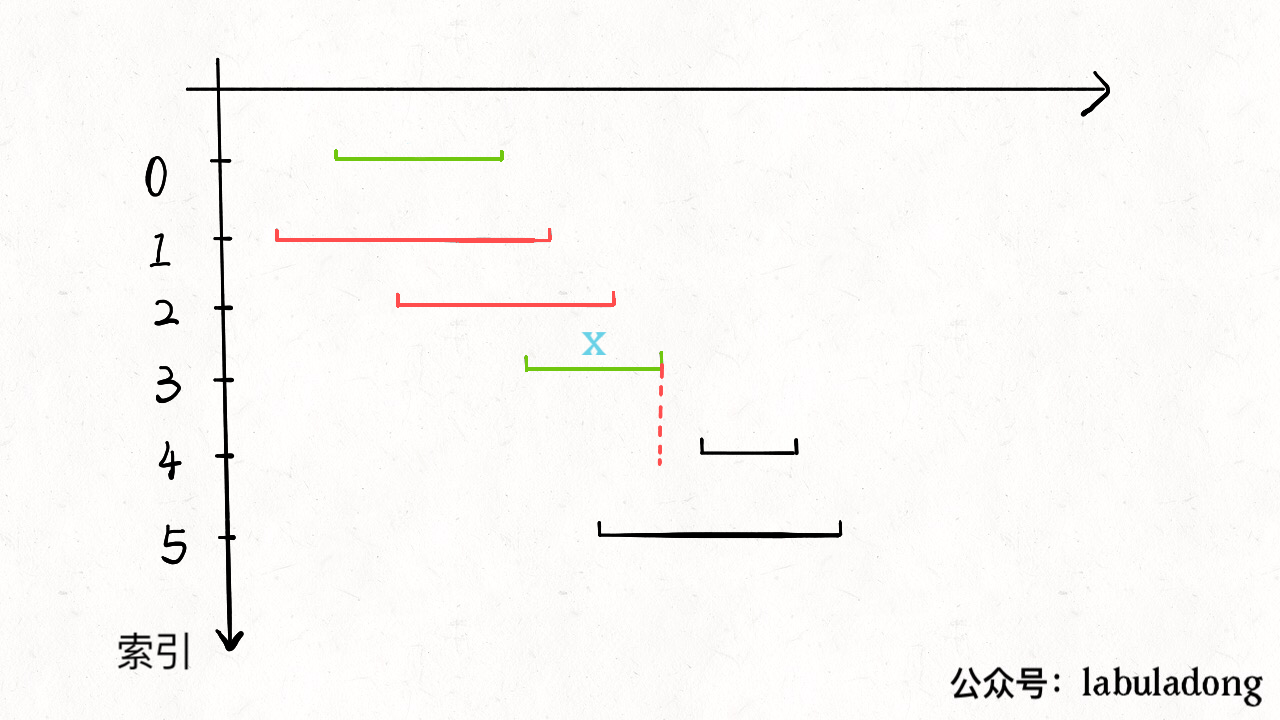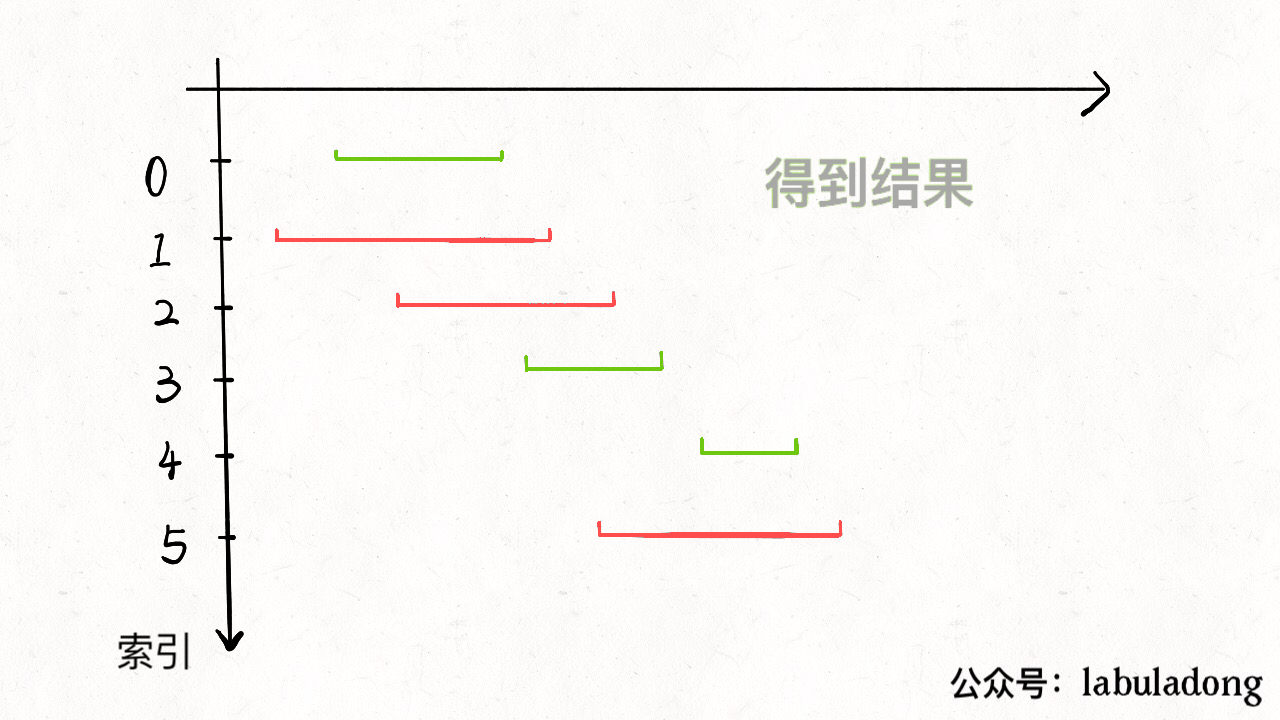
从区间集合intvs中选择一个区间x，这个x是在当前所有区间中结束最早的（end最小）
把所有与x区间相交的区间从区间集合intvs中删除
重复步骤1和2，直到intvs为空为止。之前选出的那些x就是最大不相交自己。

把这个思路实现成算法的话，可以按每个区间end数值升序排序，因为这样处理之后实现步骤1和步骤2都方便很多。

Code：

class Solution {
public:
    int eraseOverlapIntervals(vector<vector<int>>& intervals) {
        if(intervals.size() <= 1) {
            return 0;
        }
        sort(intervals.begin(), intervals.end(), [](const vector<int>& a, const vector<int>& b) {
            if(a[1] < b[1]) return true;
            if(a[1] == b[1] && a[0] < b[0]) return true;
            return false;
        });
        int right = intervals[0][1];
        int count = 0;
        for(int i = 1;i < intervals.size();i++) {
            if(intervals[i][0] < right) {
                count++;
            } else {
                right = intervals[i][1];
            }
        }
        return count;
    }
};