Celery's Blog

0%

LeetCode-Day26

发表于 更新于 Valine：

164. 最大间距

给定一个无序的数组，找出数组在排序之后，相邻元素之间最大的差值。

如果数组元素个数小于 2，则返回 0。

示例 1:

1
2
3
输入: [3,6,9,1]
输出: 3
解释: 排序后的数组是 [1,3,6,9], 其中相邻元素 (3,6) 和 (6,9) 之间都存在最大差值 3。

示例 2:

1
2
3
输入: [10]
输出: 0
解释: 数组元素个数小于 2，因此返回 0。

说明:

你可以假设数组中所有元素都是非负整数，且数值在 32 位有符号整数范围内。
请尝试在线性时间复杂度和空间复杂度的条件下解决此问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
class Solution {
public:
    // 保存最大位数
    int maxbit(vector<int> nums, int n) {
        int d = 1, p = 10;
        for(int i = 0;i < n;i++) {
            while(nums[i] >= p) {
                d++;
                p *= 10;
            }
        }
        return d;
    }
	
    // 基数排序
    void radixSort(vector<int>& nums, int n) {
        int d = maxbit(nums, n);
        int size = nums.size();
        int temp[size];
        int count[10] = {0};
        int radix = 1;
        // 进行d次排序
        for(int i = 0;i < d;i++) {
            // 每次排序前清空计算器
            for(int j = 0;j < 10;j++) {
                count[j] = 0;
            }
            // 统计每个桶中的计数器
            for(int j = 0;j < n;j++) {
                count[(nums[j] / radix) % 10]++;
            }
            // 将temp中的位置一次分配给每个桶
            for(int j = 1;j < 10;j++) {
                count[j] += count[j - 1];
            }
            // 先按照个位上的数字大小放到相应的桶中，注意这边是倒着来的！！
            for(int j = n - 1;j >= 0;j--) {
                temp[--count[(nums[j] / radix) % 10]] = nums[j];
            }
            // 收集数据
            for(int j = 0;j < n;j++) {
                nums[j] = temp[j];
            }
            radix *= 10;
        }
    }

    int maximumGap(vector<int>& nums) {
        if(nums.size() <= 1) {
            return 0;
        } 
        radixSort(nums, nums.size());
        int maxGap = nums[1] - nums[0];
        for(int i = 2;i < nums.size();i++) {
            maxGap = max(maxGap, nums[i] - nums[i - 1]);
        }
        return maxGap;
    }
};

解释：这里采用的是桶排序（基数排序）

基数排序详解：

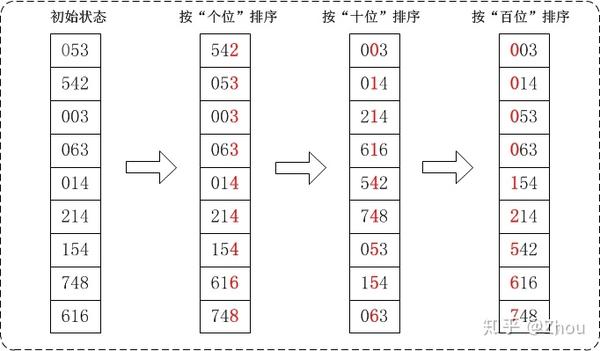
假设我们有输入数组A {53, 3, 542, 748, 14, 214, 154, 63, 616}. 这里数组位数比较小，所以我们采用LSD 的基数排序。

我们这里先在数位较短的数前面的位数上补上零，比如53补上至053，3补上至003，14补上至014，63补上至063。现在的数组表现形式为{053, 003, 542, 748, 014, 214, 154, 063, 616}。我们将它们放置至一个个单独的桶中。

现在我们首先按照“个位”上数字大小对数组中的数进行排序，排序后结果是{542, 053, 003, 063, 014, 214, 154, 616, 748}.

接着按照“十位”上数字大小对数组中的数进行排序，排序后结果是{003, 014, 214, 616, 542, 748, 053, 154, 063}.

最后按照“百位”上数字大小对数组中的数进行排序，排序后结果是{003, 014, 053, 063, 154, 214, 542, 616, 748}. 这也是我们的最终输出数组B。

img