LeetCode-Day24

148. 排序链表

在 $O(nlogn)$ 时间复杂度和常数级空间复杂度下，对链表进行排序。

示例 1:

输入: 4->2->1->3
输出: 1->2->3->4

示例 2:

输入: -1->5->3->4->0
输出: -1->0->3->4->5

思路：

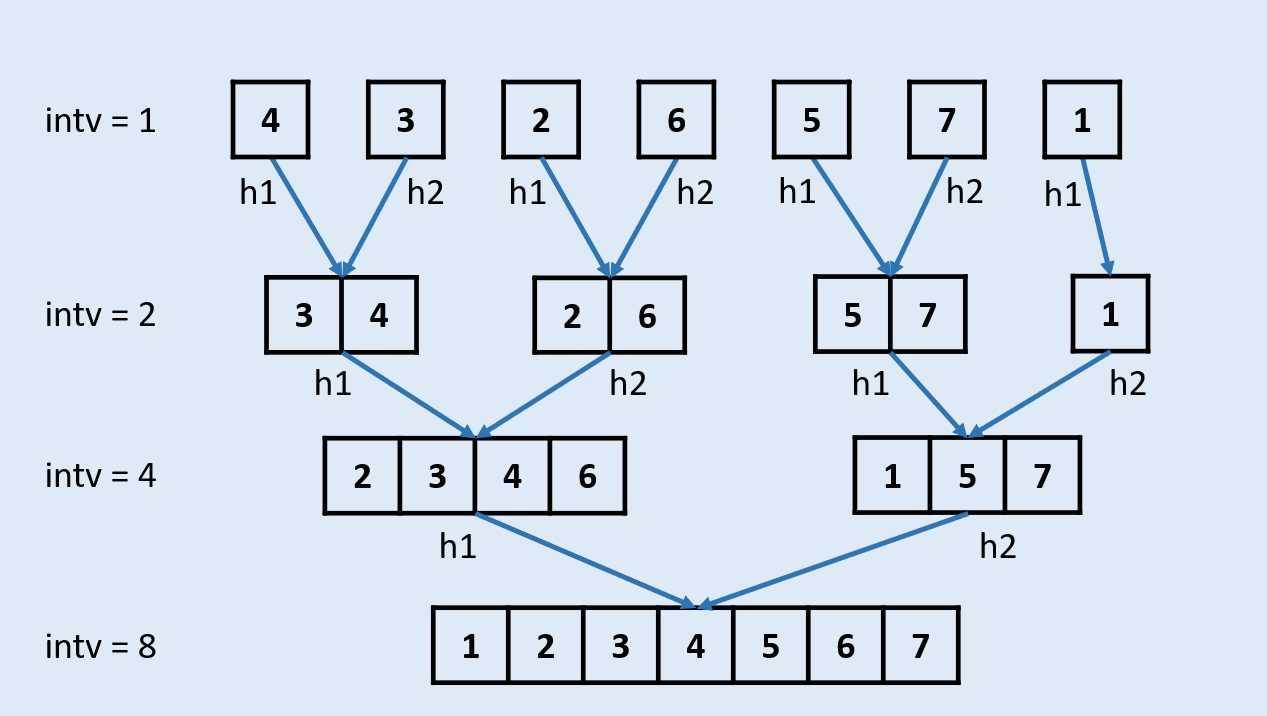
因为时间复杂度是$O(nlogn)$，所以就会想到归并排序，但是常数级空间复杂度又限制了不能采用递归，因此：

定义了三个函数:

• ListNode* sortList(ListNode* head)：用于进行归并排序

• ListNode* cut(ListNode* head, int size)： 用于拆分，从head节点开始，拆分size长度，即进行如下图的操作：

  

• ListNode* merge(ListNode* l1, ListNode* l2)：应该是闭着眼睛都会写的，归并两个有序链表。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    ListNode* sortList(ListNode* head) {
        int length = 0;
        ListNode* tempH = new ListNode(0);
        tempH->next = head;
        ListNode* lenP = head;
        while(lenP) {
            length++;
            lenP = lenP->next;
        }
        // 先计算链表的总长度为length
        for(int size = 1;size < length;size <<= 1) {
            // 总共进行logn次排序
            ListNode* H = tempH;
            ListNode* cur = H->next;
            while(H->next) {
                // left表示l1, right表示l2，cur表示l2之后的一个节点 
                ListNode* left = cur;
                ListNode* right = cut(left, size);
                cur = cut(right, size);
                // 进行归并操作
                H->next = merge(left, right);
                // 将H挪到归并之后的前一段链表的尾节点
                while(H->next) {
                    H = H->next;
                }
                // 将两段链表连接起来
                H->next = cur;
            }
        }
        return tempH->next;
    }

    ListNode* cut(ListNode* head, int size) {
        ListNode* temp = head;
        while(--size && temp)  {
            temp = temp->next;
        }
        ListNode* last = temp;
        if(!temp) {
            return NULL;
        }
        temp = temp->next;
        last->next = NULL;
        return temp;
    }

    ListNode* merge(ListNode* l1, ListNode* l2) {
        ListNode* head = new ListNode(0);
        ListNode* temp = head;
        while(l1 && l2) {
            if(l1->val < l2->val) {
                temp->next = l1;
                l1 = l1->next;
            } else {
                temp->next = l2;
                l2 = l2->next;
            }
            temp = temp->next;
        }
        temp->next = l1 ? l1 : l2;
        return head->next;
    }
};

图解：

146. LRU缓存机制

运用你所掌握的数据结构，设计和实现一个 LRU (最近最少使用) 缓存机制。它应该支持以下操作： 获取数据 get 和 写入数据 put 。

获取数据 get(key) - 如果密钥 (key) 存在于缓存中，则获取密钥的值（总是正数），否则返回 -1。
写入数据 put(key, value) - 如果密钥不存在，则写入其数据值。当缓存容量达到上限时，它应该在写入新数据之前删除最近最少使用的数据值，从而为新的数据值留出空间。

进阶:

你是否可以在 O(1) 时间复杂度内完成这两种操作？

示例:

LRUCache cache = new LRUCache( 2 /* 缓存容量 */ );

cache.put(1, 1);
cache.put(2, 2);
cache.get(1);       // 返回  1
cache.put(3, 3);    // 该操作会使得密钥 2 作废
cache.get(2);       // 返回 -1 (未找到)
cache.put(4, 4);    // 该操作会使得密钥 1 作废
cache.get(1);       // 返回 -1 (未找到)
cache.get(3);       // 返回  3
cache.get(4);       // 返回  4

思路详解：

要让 put 和 get 方法的时间复杂度为 O(1)O(1)，我们可以总结出 cache 这个数据结构必要的条件：查找快，插入快，删除快，有顺序之分。

因为显然 cache 必须有顺序之分，以区分最近使用的和久未使用的数据；而且我们要在 cache 中查找键是否已存在；如果容量满了要删除最后一个数据；每次访问还要把数据插入到队头。

那么，什么数据结构同时符合上述条件呢？哈希表查找快，但是数据无固定顺序；链表有顺序之分，插入删除快，但是查找慢。所以结合一下，形成一种新的数据结构：哈希链表。

LRU 缓存算法的核心数据结构就是哈希链表，双向链表和哈希表的结合体。这个数据结构长这样：

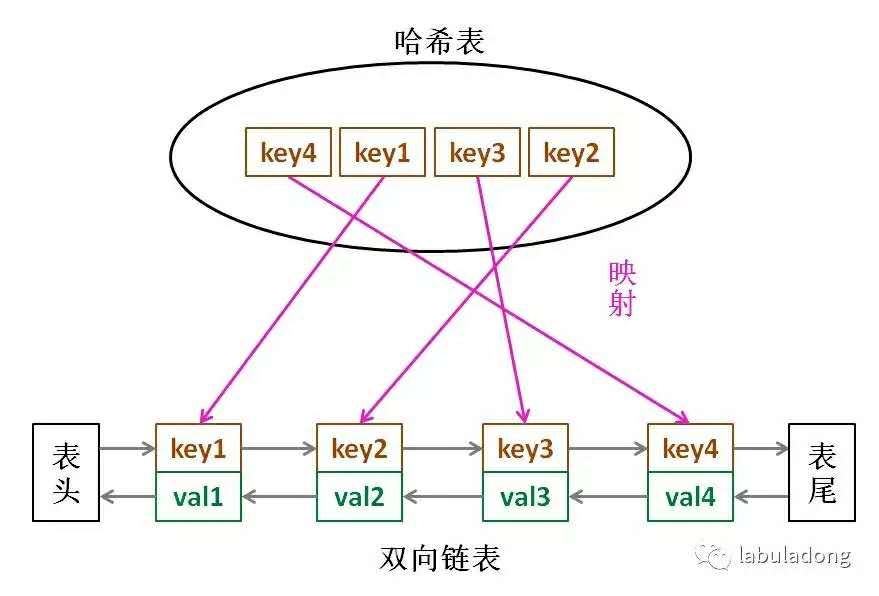
思想很简单，就是借助哈希表赋予了链表快速查找的特性嘛：可以快速查找某个 key 是否存在缓存（链表）中，同时可以快速删除、添加节点。回想刚才的例子，这种数据结构是不是完美解决了 LRU 缓存的需求？

class LRUCache {
private:
    int cap;
    // 双链表： 装着(key, value)元组
    list<pair<int, int>> cache;
    unordered_map<int, list<pair<int, int>>::iterator> map;
public:
    LRUCache(int capacity) {
        this->cap = capacity;
    }

    int get(int key) {
        auto it = map.find(key);
        if(it == map.end()) {
            return -1;
        }
        pair<int, int> kv = *map[key];
        cache.erase(map[key]);
        cache.push_front(kv);
        map[key] = cache.begin();
        return kv.second;
    }

    void put(int key, int value) {
        auto it = map.find(key);
        if(it == map.end()) {
            // key不存在，判断cache是否已满
            if(cache.size() == cap) {
                auto lastPair = cache.back();
                int lastKey = lastPair.first;
                map.erase(lastKey);
                cache.pop_back();
            }
            cache.push_front(make_pair(key, value));
            map[key] = cache.begin();
        } else {
            cache.erase(map[key]);
            cache.push_front(make_pair(key, value));
            map[key] = cache.begin();
        }
    }
};

149. 直线上最多的点数

给定一个二维平面，平面上有 n 个点，求最多有多少个点在同一条直线上。

示例 1:

输入: [[1,1],[2,2],[3,3]]
输出: 3
解释:
^
|
|        o
|     o
|  o  
+------------->
0  1  2  3  4

示例 2:

输入: [[1,1],[3,2],[5,3],[4,1],[2,3],[1,4]]
输出: 4
解释:
^
|
|  o
|     o        o
|        o
|  o        o
+------------------->
0  1  2  3  4  5  6

思路：

针对每一个点，利用hashmap，然后遍历每一个点，计算斜率，利用hashmap检查该斜率是否已经出现过，然后更新hashmap

这里需要注意的是精度问题！因为斜率计算的时候是double类型。

class Solution {
public:
    int maxPoints(vector<vector<int>>& points) {
        if(points.size() <= 2) {
            return points.size();
        }
        map<long long, int> mp;
        int ans = 0;
        for(int i = 0;i < points.size();i++) {
            mp.clear();
            int col = 1, tp = 0;
            for(int j = i + 1;j < points.size();j++) {
                int dely = points[j][1] - points[i][1];
                int delx = points[j][0] - points[i][0];
                if(delx == 0 && dely == 0)  {
                    col++;
                    continue;
                }
                int gcd = __gcd(delx, dely);
                dely = dely / gcd;
                delx = delx / gcd;
                long long hash = 1ll * delx * 1000000 + dely;
                // cout << "hash = " << hash << endl; 
                if(mp.count(hash) == 0) {
                    mp[hash] = 1;
                    tp = max(tp, mp[hash]);
                } else {
                    mp[hash]++;
                    tp = max(tp, mp[hash]);
                }
            }
            ans = max(ans, tp + col);
            // cout << "ans = " << ans << endl;
        }
        return ans;
    }
};

152. 乘积最大子序列

给定一个整数数组 nums ，找出一个序列中乘积最大的连续子序列（该序列至少包含一个数）。

示例 1:

输入: [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。

示例 2:

输入: [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

思路：这里还是才有用动态规划的思路，但是需要注意，仅仅用一个dp是不够的，因为你可能遇到的是如下数据：

[-2,3,-4]

如果只有一个dp[]，则你记录下的dp[]的值为[-2,3,3]

因为忽略了负数乘以负数得到最大值的情形，，因此下面的方法记录了两个dp数组，分别是dpmin[],dpmax，这样，就可以顺利解决刚刚的bug了。

Code如下：

class Solution {
public:
    int maxProduct(vector<int>& nums) {
        if(nums.size() == 1) {
            return nums[0];
        }        
        int ans = nums[0];
        vector<int> dpmax(nums.size(), 0);
        vector<int> dpmin(nums.size(), 0);
        dpmax[0] = ans;
        dpmin[0] = ans;
        for(int i = 1;i < nums.size();i++) {
            dpmax[i] = max(dpmax[i - 1] * nums[i], max(dpmin[i - 1] * nums[i], nums[i]));
            dpmin[i] = min(dpmin[i - 1] * nums[i], min(dpmax[i - 1] * nums[i], nums[i]));
            ans = max(ans, dpmax[i]);
        }
        return ans;    
    }
};

155. 最小栈

设计一个支持 push，pop，top 操作，并能在常数时间内检索到最小元素的栈。

push(x) – 将元素 x 推入栈中。
pop() – 删除栈顶的元素。
top() – 获取栈顶元素。
getMin() – 检索栈中的最小元素。
示例:

MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

思路：

一般来说，为了做到提取最小值，一般采用的是$O(n)$的做法，但是，为了做到$O(1)$的解法，我们可以有以下思路：

就是在每一次push的时候push两个值，一个是当前的x，另一个是当前的最小值，而push进去的最小值只需要在之前的最小值和x之间选择较小的一个即可。pop的时候同理，每次pop两个元素。而这样在去的最小值的时候，可以直接取栈顶元素。

class MinStack {
private:
    int index = -1;
    int length;
    int nums[20000];
public:
    /** initialize your data structure here. */
    MinStack() {
        
    }
    
    void push(int x) {
        nums[++index] = x;
        if(index == 0) {
            nums[++index] = x; 
        } else {
            nums[++index] = min(x, nums[index - 1]);   
        }
    }
    
    void pop() {
        index -= 2;
    }
    
    int top() {
        return nums[index - 1];
    }
    
    int getMin() {
        return nums[index];
    }
};