LeetCode-Day23

135. 分发糖果

老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。

你需要按照以下要求，帮助老师给这些孩子分发糖果：

每个孩子至少分配到 1 个糖果。
相邻的孩子中，评分高的孩子必须获得更多的糖果。
那么这样下来，老师至少需要准备多少颗糖果呢？

示例 1:

1
2
3

输入: [1,0,2]
输出: 5
解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。

示例 2:

输入: [1,2,2]
输出: 4
解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。
     第三个孩子只得到 1 颗糖果，这已满足上述两个条件。

思路：只需要扫一遍数组

如何判断i位置需要所少糖果，我们需要处理的有三种情况：

ratings[i - 1] == ratings[i]，那么我们只需要1颗糖果
ratings[i - 1] < ratings[i]，那么，我们只需要比前一个多一个糖果即可。

ratings[i - 1] > ratings[i]，此时，我们不知道该如何判断了

但是，如果我们知道递减的个数，我们就能判断，当前的i(即局部最高点)需要多少糖果了

所以，我们保证，递减序列，是从1开始加的（方向加），例如：

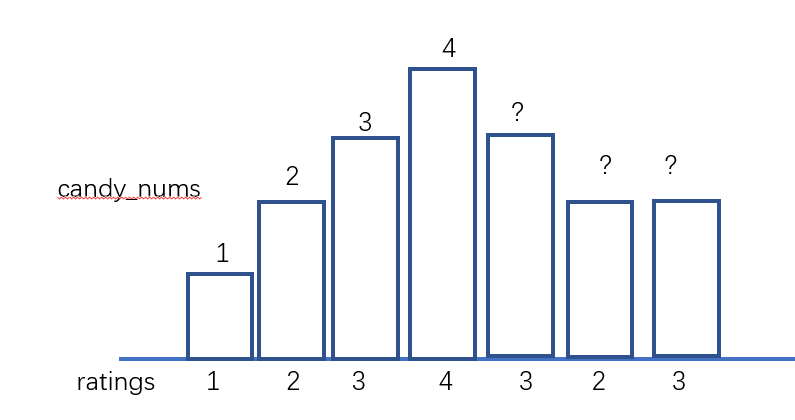
如何判断?位置的糖果有多少，我们发现ratings是3-2递减的，递减序列个数des_num ，我们反向加，有公差为1的求和公式：（首项 + 尾项） * 项数 / 2，所以我们先假设ratings在等于4的时候，也是满足等差的，那么就有(1 + des_num) * des_num / 2 = (1 + 2) * 2 / 2 = 3颗糖果，是3-2 需要的糖果数：2-1

**但是，**还有一种情况，如下

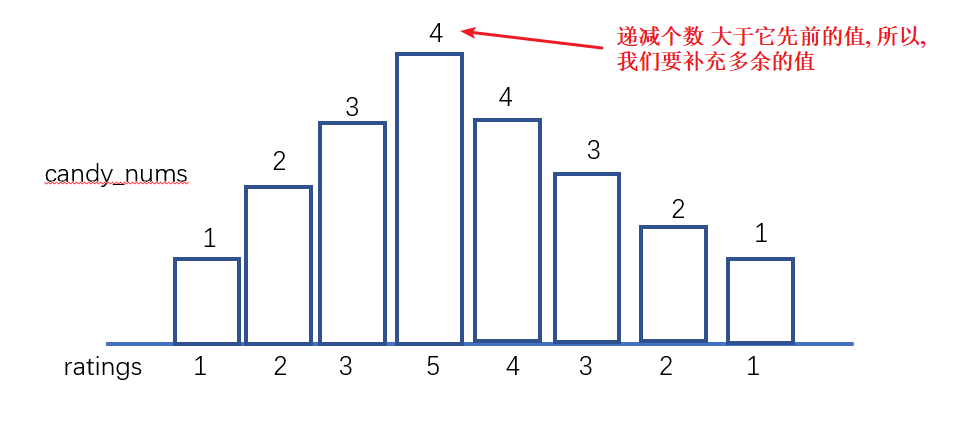
也就是最高点的位置的糖果数不够，则此时，只需要变更最高点的糖果数目即可。

所以，时间复杂度是 $O(n)$ ，空间复杂度是 $O(1)$

上Code:

class Solution {
public:
    int candy(vector<int>& ratings) {
        int maxCandy = 1, sum = 1, des_num = 0;
    for(int i = 1;i < ratings.size();i++) {
        if(ratings[i] >= ratings[i - 1]) {
            if(des_num > 0) {
                sum += (1 + des_num) * des_num / 2;
                if(maxCandy <= des_num) {
                    sum += (des_num - maxCandy + 1);
                }
                des_num = 0;
                maxCandy = 1;
            }
            maxCandy = ratings[i] == ratings[i - 1] ? 1 : maxCandy + 1;
            sum += maxCandy;
        } else {
            des_num++;
        }
    }
    if(des_num > 0) {
        sum += (1 + des_num) * des_num / 2;
        if(maxCandy <= des_num) {
            sum += (des_num - maxCandy + 1);
        }
    }
    return sum;
    }
};

136. 只出现一次的数字

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现两次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？

示例 1:

1 2	输入: [2,2,1] 输出: 1

示例 2:

1 2	输入: [4,1,2,1,2] 输出: 4

一开始能想到的估计也就是Hash。但是看到评论区的大神，真的是很绝了。

方法一：数学

2*(a + b + c) - (a + a + b + b + c) - c

看完这个应该知道该怎么写了吧，但是这里需要用到set，空间复杂度是 $O(n)$

int singleNumber(vector<int>& nums) {
    int sum1 = 0, sum2 = 0;
    set<int> unique;
    for(int i = 0;i < nums.size();i++) {
        sum1 += nums[i];
        unique.insert(nums[i]);
    }
    for(set<int>::iterator it = unique.begin();it != unique.end();it++) {
        sum2 += *it;
    } 
    return 2 * sum2 - sum1;
}

方法二：位运算

概念：

我们如果对0和二进制位做XOR运算，得到的仍然是这个二进制位
- a ⊕ 0 = a
我们如果对相同的二进制位做XOR运算，返回的结果是0
- a ⊕ a = 0
XOR满足交换律和结合律

综上，只要将nums里面的所有数字相异或，即可得到最终答案：

因为只要出现过两次，这两个数字的异或结果就是0,0和任何数字异或仍然是0，所以一伙完之后，凡是一对出现的，结果都是0，只剩下出现过一次的数字和0进行异或，还是它本身，因此，最终结果就是只出现一次的数字。

位运算大法好！

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int a = nums[0];
        for(int i = 1;i < nums.size();i++) {
            a = a ^ nums[i];
        }
        return a;
    }
};

通用解法：

原问题：数组中某数出现k次，k>=2，有一数出现一次，求出该数

解法：

使用一个32维的数组，用这个32维的数组存储所有数里面的第0位1的总数，第一位1的总数…第31位1的总数

假如第0位1的个数是k的倍数，那么要求的这个数在该位一定是0，若不是k的倍数，那么要求的这个数在改为一定是1，第1位的1一直到第31位的1的个数同理。

所以在下一个进阶的题目中：

137. 只出现一次的数字II

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。

说明：

你的算法应该具有线性时间复杂度。你可以不使用额外空间来实现吗？

示例 1:

1 2	输入: [2,2,3,2] 输出: 3

示例 2:

1 2	输入: [0,1,0,1,0,1,99] 输出: 99

直接上通用Code：

class Solution {
public:
    int singleNumber(vector<int>& nums) {
        int ans = 0;
        int temp[32] = {0};
        int i, j;
        for(int k = 0;k < nums.size();k++) {
            i = 1, j = 31;
            while(j >= 0) {
                if(nums[k] & i) {
                    temp[j]++;
                }
                // 注意一下这边的问题，如果不加if条件，则有可能过不了编译，因为最后一次左移是在i已经是最小值的情况下面的，所以可能会导致溢出。
                if(i != INT_MIN) {
                    i <<= 1;   
                }
                j--;
            }
        }
        j = 0;
        while(j <= 31) {
            if(temp[j] % 3 != 0) {
                ans += 1;
            }
            if(j != 31) {
                ans <<= 1;
            }
            j++;
        }
        cout << ans;
        return ans;
    }
};

仅仅针对这道题而言，会有更加快速的方法：

即三进制下不考虑进位的加法：过定义某种运算 #，使得 0 # 1 = 1，1 # 1 = 2，2 # 1 = 0。在此运算规则下，出现了 33 次的数字的二进制所有位全部抵消为 00，而留下只出现 11 次的数字二进制对应位为 11。因此，在此运算规则下将整个arr中数字遍历加和，留下来的结果则为只出现 11 次的数字。

代码分析：

ones ^= num;：记录至目前元素num，二进制某位出现1次（当某位出现3次，有ones = 1, twos = 1共同表示出现3次）
twos |= ones & num：记录至目前元素num，二进制某位出现2次（当某位出现2次时，twos = 1, ones = 0）
threes = ones & twos：记录至目前元素num，二进制某位出现3次（即当ones 和twos对应位同时为1时，three为1）
ones &= ~threes, two &= ~threes：将ones，twos中出现了3次的对应位清零，实现“不考虑进位的三进制加法”

1
2

141. 环形链表

给定一个链表，判断链表中是否有环。

为了表示给定链表中的环，我们使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

示例 2：

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    bool hasCycle(ListNode *head) {
        if(head == NULL) {
            return false;
        }
        ListNode *fast = head->next, *slow = head;
        while(fast != NULL && fast != slow) {
            slow = slow->next;
            if(fast->next == NULL) {
                return false;
            } 
            fast = fast->next->next;
        }
        if(fast == NULL) {
            return false;
        }
        return true;
    }
};

142. 环形链表II

在上一题的基础上，要求返回成环的起点；

一开始我想到的是先判断是否成环，然后记录下从起点到成环需要经过多少步数index，然后利用快慢指针，快指针先走index步，然后当快慢指针指向同一个地方的时候，就是成环的起点。

后来发现并不需要这么做，经过推导之后，会发现从它们相遇的起点开始，将慢指针重新定位为head，然后一起走，遇到一起的时候，就是成环的起点。

推导如下：

![img](file:///C:\Users\12751\Documents\Tencent Files\1275121799\Image\C2C{0F01A453-1C35-54CA-5C5C-23816865D293}.png)

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        if(head == NULL || head->next == NULL) {
            return NULL;
        }
        ListNode *fast = head->next->next, *slow = head->next;
        while(fast != NULL && fast != slow) {
            slow = slow->next;
            if(fast->next == NULL) {
                return NULL;
            } 
            fast = fast->next->next;
        }
        if(fast == NULL) {
            return NULL;
        }
        // cout << fast->val << endl;
        slow = head;
        while(fast != slow) {
            fast = fast->next;
            slow = slow->next;
        }
        return slow;     
    }   
};

143. 重排链表

给定一个单链表 L：L0→L1→…→Ln-1→Ln ，
将其重新排列后变为： L0→Ln→L1→Ln-1→L2→Ln-2→…

你不能只是单纯的改变节点内部的值，而是需要实际的进行节点交换。

示例 1:

1	给定链表 1->2->3->4, 重新排列为 1->4->2->3.

示例 2:

1	给定链表 1->2->3->4->5, 重新排列为 1->5->2->4->3.

思路：

先利用快慢指针，快指针走两步，慢指针走一步，当快指针到达最后的时候，慢指针到达中间，然后将后半部分链表进行倒序。最后合并两个链表。

即：设原链表为1->2->3->4

分成两部分1->2 3->4

将后面倒序4->3

然后合并两个链表1->4->2->3

Code如下：

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode(int x) : val(x), next(NULL) {}
 * };
 */
class Solution {
public:
    void reorderList(ListNode* head) {
    if(head == NULL || head->next == NULL) {
        return ;
    }
    ListNode* fast = head;
    ListNode* slow = head;
    while(fast != NULL && fast->next != NULL) {
        fast = fast->next->next;
        slow = slow->next;
    }
    // slow = slow->next;
    cout << slow->val;
    ListNode* temp = slow;
    ListNode* last = NULL;
    while(slow != NULL) {
        slow = slow->next;
        temp->next = last;
        last = temp;
        temp = slow;
    }
    //此时last指向的就是链表头
    ListNode* aft1 = head, *aft2 = last;
    ListNode* pre1 = aft1->next, *pre2 = aft2->next;
    while(pre1 != NULL && pre2 != NULL) {
        aft1->next = aft2;
        aft2->next = pre1;
        aft1 = pre1, aft2 = pre2;
        pre1 = pre1->next;
        pre2 = pre2->next;
    }
    return ;
    }
};