Celery's Blog

0%

LeetCode-Day21

发表于 Valine：

91. 解码方法

一条包含字母 A-Z 的消息通过以下方式进行了编码：

1
2
3
4
'A' -> 1
'B' -> 2
...
'Z' -> 26

给定一个只包含数字的非空字符串，请计算解码方法的总数。

示例 1:

1
2
3
输入: "12"
输出: 2
解释: 它可以解码为 "AB"（1 2）或者 "L"（12）。

示例 2:

1
2
3
输入: "226"
输出: 3
解释: 它可以解码为 "BZ" (2 26), "VF" (22 6), 或者 "BBF" (2 2 6) 。

动态规划

本题利用动态规划比较容易解决，但是注意需要分情况讨论：

  • dp[i]为str[i]的译码方法总数
  • 分情况讨论：（建立最优子情况）
    • 若s[i] = '0'，那个若s[i - 1] = ‘1’ or ‘2’，则dp[i] = dp[i - 1]
      • 解释：s[i - 1] + s[i]唯一被译码，不增加情况
    • 若s[i - 1] = ‘1’，则dp[i] = dp[i - 1] + dp[i - 2]
      • 解释：s[i - 1]与s[i]分开译码，为dp[i - 1]；合并译码，为dp[i - 2]
    • 若s[i - 1] ‘2’ and ‘1’ <= s[i] <= ‘6’，则dp[i ] = dp[i - 1] + dp[i - 2]
      • 解释：同上
  • 由分析可知，dp[i]仅可能与前两项有关，故可以用单变量代替dp[] 数组，将空间复杂度从O(n) 降到 O(1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
class Solution {
public:
    int numDecodings(string s) {
        if(s[0] == '0') {
            return 0;
        }
        int pre = 1, curr = 1;
        for(int i = 1;i < s.size();i++) {
            int tmp = curr;
            if(s[i] == '0') {
                if(s[i - 1] == '1' || s[i - 1] == '2') {
                    curr = pre;
                } else {
                    return 0;
                }
            } else if(s[i - 1] == '1' || (s[i - 1] == '2' && s[i] >= '0' && s[i] <= '6')) {
                curr = curr + pre;
            }
            pre = tmp;
        }
        return curr;
    }
};

94. 二叉树的中序遍历

回顾二叉树了…

给定一个二叉树，返回它的中序 遍历。

示例:

1
2
3
4
5
6
7
8
输入: [1,null,2,3]
   1
    \
     2
    /
   3

输出: [1,3,2]

方法一. 递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
};

void Traversal(TreeNode* root, vector<int>& ans) {
    if(root != NULL) {
        Traversal(root->left, ans);
        ans.push_back(root->val);
        Traversal(root->right, ans);
    }
    
}

vector<int> inorderTraversal(TreeNode* root) {
    vector<int> ans;       
    Traversal(root, ans);
    return ans; 
}

方法二. 栈

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
vector<int> inorderTraversal2(TreeNode* root) {
    vector<int> ans;
    stack<int> st;
    TreeNode* curr = root;
    while(curr != NULL || !st.empty) {
        while(curr != NULL) {
            st.push(curr);
            curr = curr->left;
        }
        curr = st.top();
        st.pop();
        ans.push_back(curr->val);
        curr = curr->right;
    }
    return curr->right;
}

解释：

img

img

img

img

img

img

img

img

img

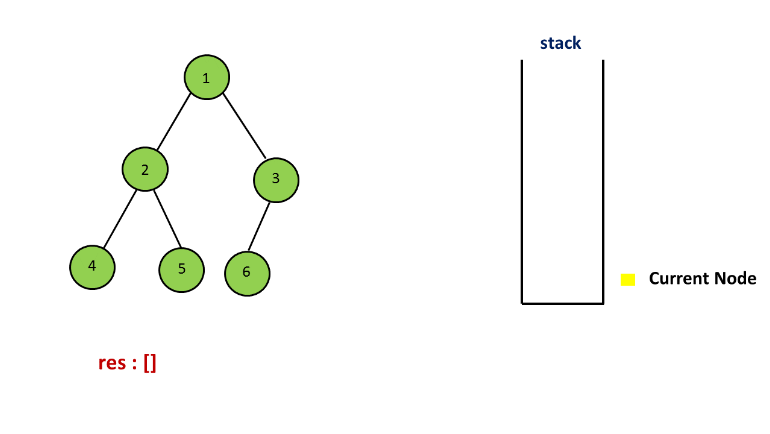
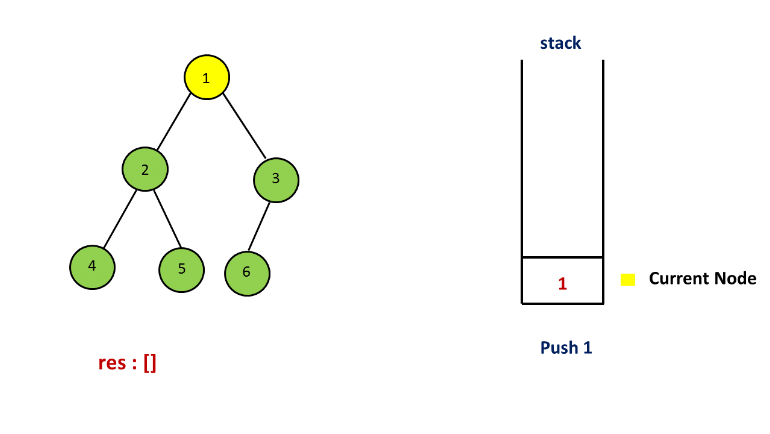
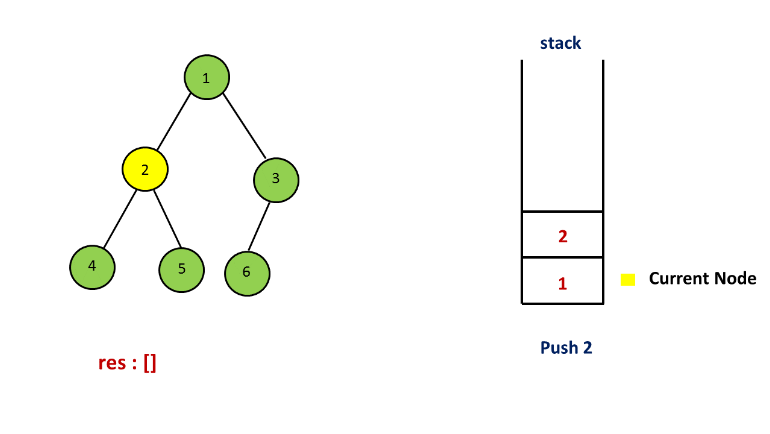
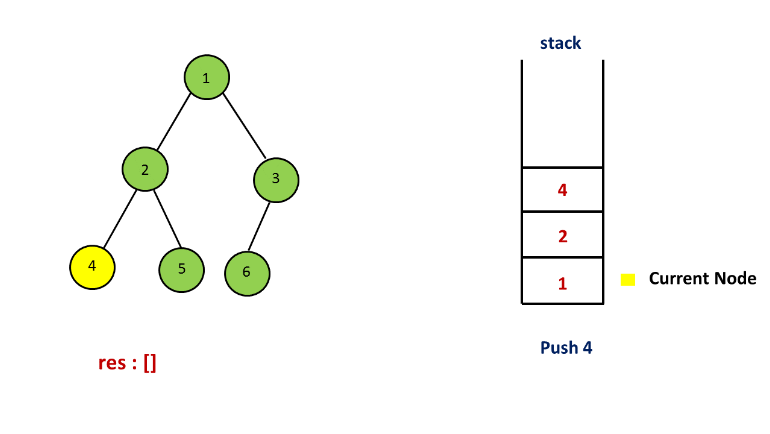
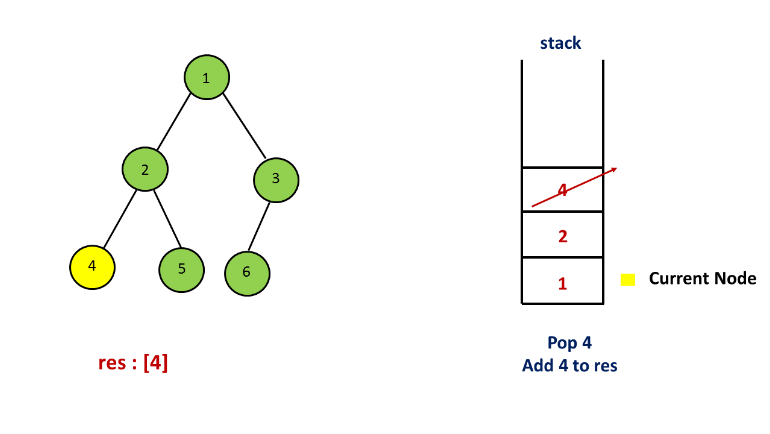
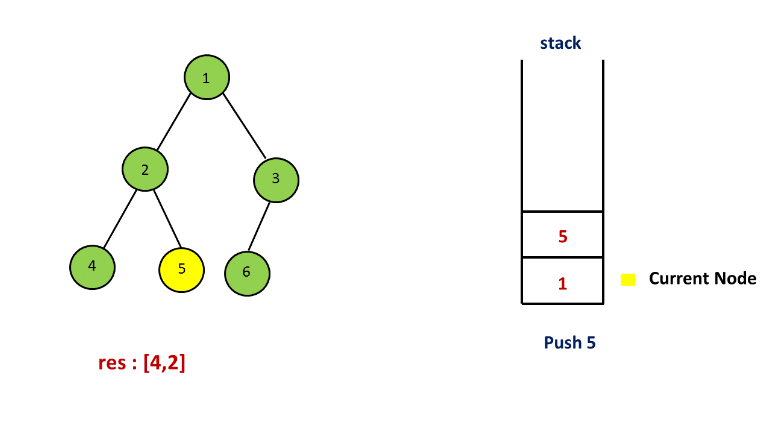
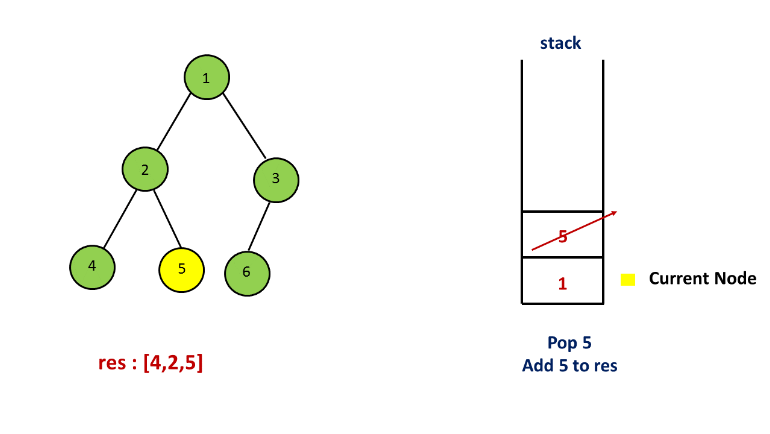
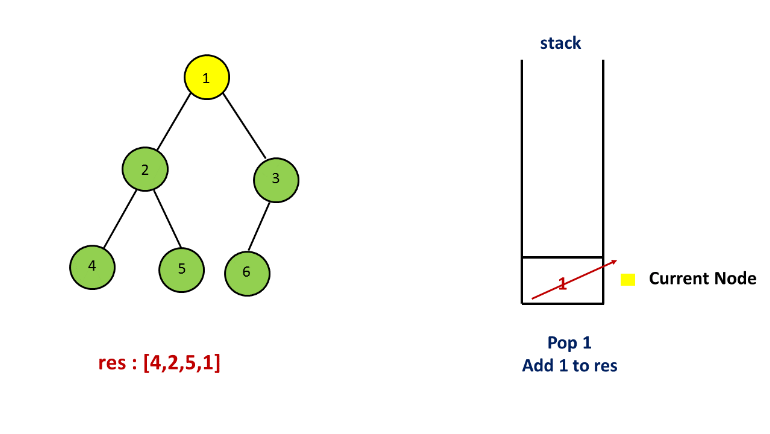
方法三. 莫里斯遍历

在该方法中，我们使用一种新的数据结构：线索二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
vector<int> inorderTraversal3(TreeNode* root) {
    vector<int> ans;
    TreeNode* curr = root;
    TreeNode* pre;
    while(curr != NULL) {
        if(curr->left == NULL) {
            ans.push_back(curr->val);
            curr = curr->right;
        } else {
            pre = curr->left;
            while(pre->right != NULL) {
                pre = pre->right;
            }
            pre->right = curr;
            TreeNode* temp = curr;
            curr = curr->left;
            temp->left = NULL;
        }
    }
    return ans;
}

这个还没学会…

96. 不同的二叉搜索树

给定一个整数 n，求以 1 … n 为节点组成的二叉搜索树有多少种？

示例:

1
2
3
4
5
6
7
8
9
10
输入: 3
输出: 5
解释:
给定 n = 3, 一共有 5 种不同结构的二叉搜索树:

   1         3     3      2      1
    \       /     /      / \      \
     3     2     1      1   3      2
    /     /       \                 \
   2     1         2                 3

这是有公式的！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class Solution {
public:
    int numTrees(int n) {
        if(n == 0) {
            return 1;
        }
        long long dp[n + 1];
        dp[0] = 1;
        for(int i = 1;i <= n;i++) {
            dp[i] = dp[i - 1] * (2 * n - (i - 1)) / i;
        }
        return dp[n] - dp[n - 1]; 
    }
};

解释：用到了递归的思想

先考虑只有一个节点的情形，设此时的形态有f(1)种，很显然，f(1) = 1

如果有两个节点呢？我们很自然的想到，应该在f(1)的基础上考虑递推关系。那么，如果固定一个节点之后，有两种情况，一是左子树还剩下一个节点，此时，类型数量为f(1)，第二种情况是右子树剩下一个节点，此时，类型数量为f(1)，故有f(2) = f(1) + f(1)

如果有三个节点呢？此时不能再固定节点了，因为当节点数量大于等于2时，无论如何固定，其形态必然有很多种，而在这多种基础之上你如何安排后续剩下的节点呢？因此必须跳出这个误区

回到二叉树的定义，二叉树本质上就是一个递归的形式，左子树，右子树，根节点。所以，根节点应该不变，需要递归处理的是左右子树。

也就是说，还要考虑固定一个节点，即根节点。按照这个思路，那么左右子树的分布情况为 2 = 0 + 2 = 1 + 1 = 2 + 0

所以，有3个节点的时候，递归形式为f(3) = f(2) + f(1) * f(1) + f(2)（注意这里的乘法，因为左右子树一起组成整棵树，所以根据排列组合里面的乘法原理即可得出）

那么有n个节点时呢？我们固定一个节点，那么左右子树的分布情况为

n - 1 = n - 1 + 0 = n - 2 + 1 = n - 3 + 2 = ... = 1 + n - 2 = 0 + n - 1

OK，所以递归表达式就出来了

f(n) = f(n - 1) + f(n - 2) * f(1) + f(n - 3) * f(2) + ... + f(1) + f(n - 2) + f(n - 1)

通项公式为：f(n) = 1/(n+1)*C(n, 2n) = C(n, 2n) - C(n - 1, 2n), n = 0, 1, 2...

前几个数字为1,1,2,5,14,42,132

98. 验证二叉搜索树

给定一个二叉树，判断其是否是一个有效的二叉搜索树。

假设一个二叉搜索树具有如下特征：

节点的左子树只包含小于当前节点的数。
节点的右子树只包含大于当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:

1
2
3
4
5
输入:
    2
   / \
  1   3
输出: true

示例 2:

1
2
3
4
5
6
7
8
9
输入:
    5
   / \
  1   4
     / \
    3   6
输出: false
解释: 输入为: [5,1,4,null,null,3,6]。
     根节点的值为 5 ，但是其右子节点值为 4 。

方法：中序遍历即可，只要数字是从小到大排列的就好，下面用了栈来解决中序遍历的问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> st;
        double inorder = -DBL_MAX;
        while(!st.empty() || root != NULL) {
            while(root != NULL) {
                st.push(root);
                root = root->left;
            }
            root = st.top();
            st.pop();
            if(root->val <= inorder) {
                return false;
            }
            inorder = root->val;
            root = root->right;
        }
        return true;
    }
};

注意：这里有一个巨大无比的坑，就是这里的最小值的表示，如果使用int inorder = INT_MIN，就会出bug，就算是用double inorder = DLB_MIN也会出问题，只能使用double inorder = -DBL_MAX，这是为什么呢？

1
2
#define DBL_MAX 1.7976931348623158e+308 // max value 
#define DBL_MIN 2.2250738585072014e-308 // min positive value