85. 最大矩形
给定一个仅包含 0 和 1 的二维二进制矩阵,找出只包含 1 的最大矩形,并返回其面积。
示例:
1 | 输入: |
方法一. 动态规划——使用柱状图的优化暴力算法
算法
我们可以以常数时间计算出在给定的坐标结束的矩形的最大宽度。我们可以通过记录每一行中每一个方块连续的“1”的数量来实现这一点。每遍历完一行,就更新该点的最大可能宽度。通过以下代码即可实现。 row[i] = row[i - 1] + 1 if row[i] == '1'.
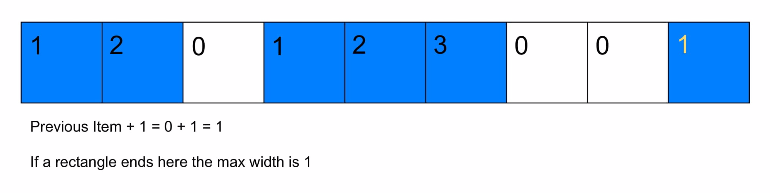
一旦我们知道了每个点对应的最大宽度,我们就可以在线性时间内计算出以该点为右下角的最大矩形。当我们遍历列时,可知从初始点到当前点矩形的最大宽度,就是我们遇到的每个最大宽度的最小值。
我们定义:
$curArea = maxWidth * (curre***ow - originalRow + 1)
curArea=maxWidth∗(curre∗∗∗ow−originalRow+1)$
$maxArea = max(maxArea, curArea)
$$maxArea=max(maxArea,curArea)$
下面的动画有助于理解。给定每个点的最大宽度,可计算出底端黄色方块的最大矩形面积。
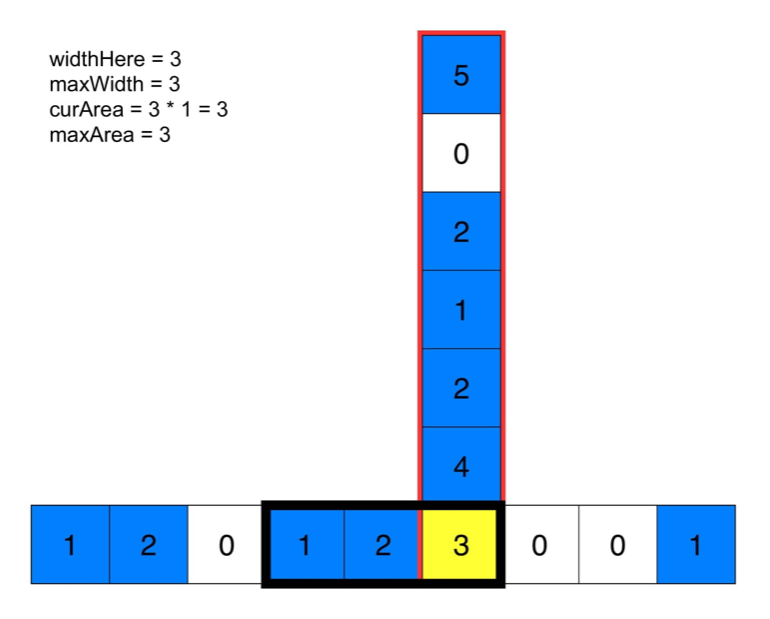
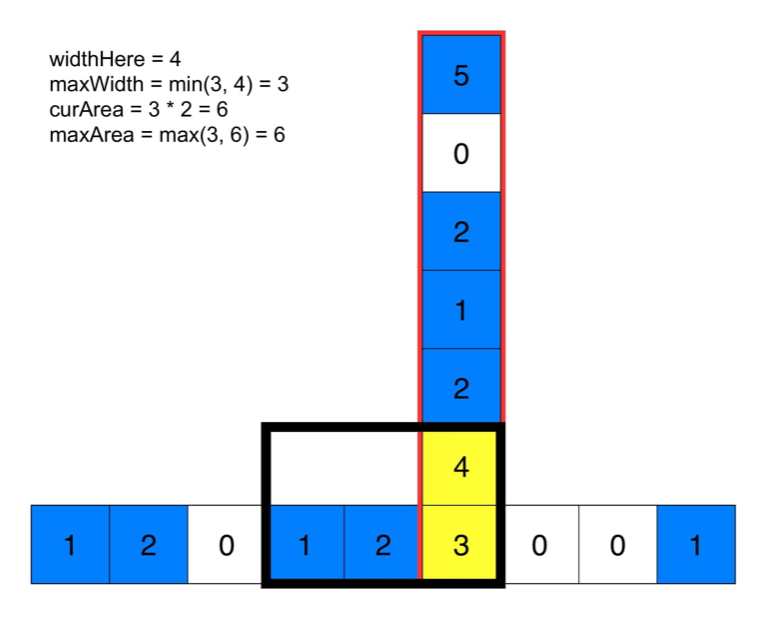
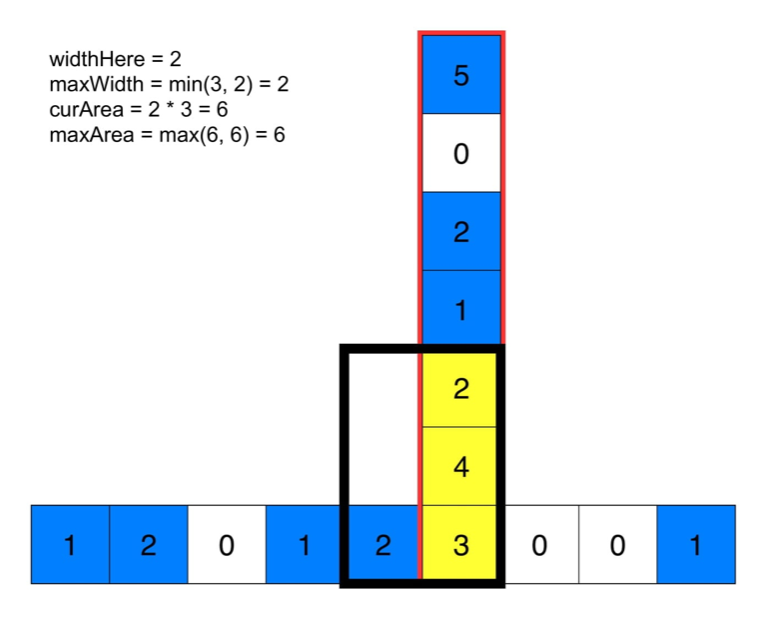
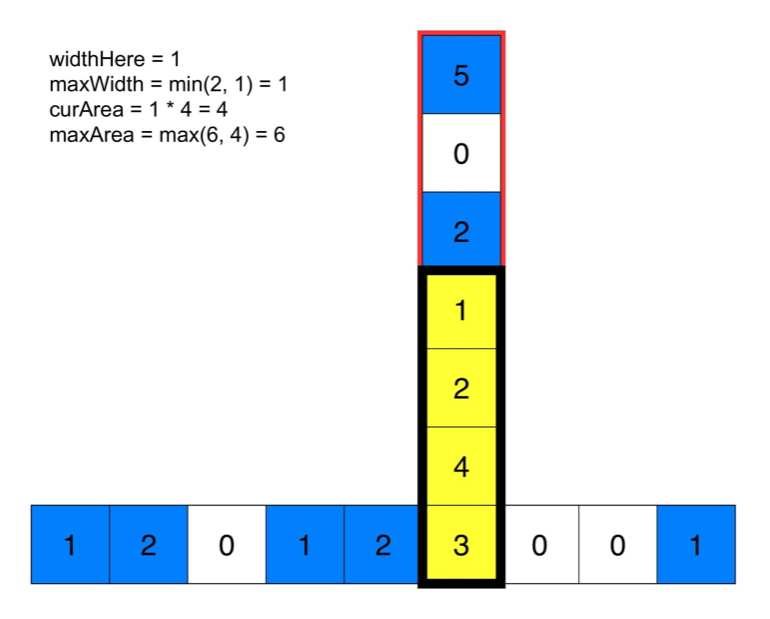
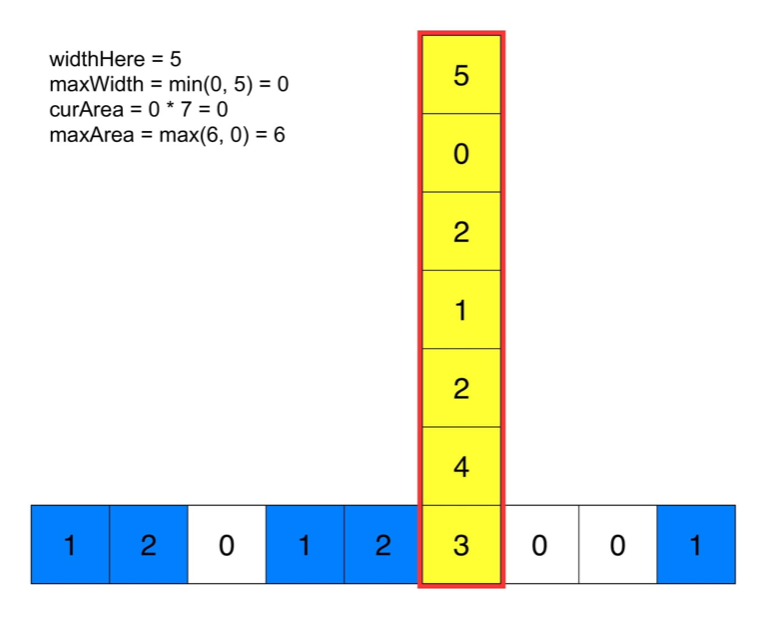
对每个点重复这一过程,就可以得到全局最大。
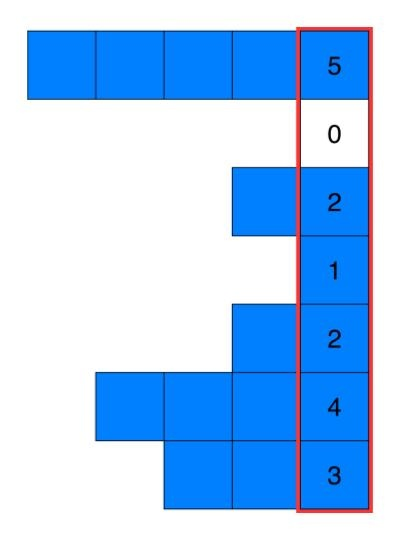
注意,我们预计算最大宽度的方法事实上将输入转化成了一系列的柱状图,每一栏是一个新的柱状图。我们在针对每个柱状图计算最大面积。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21int maximalRectangle(vector<vector<char>>& matrix) {
if(matrix.size() == 0) {
return 0;
}
vector<vector<int>> dp(matrix.size(), vector<int>(matrix[0].size(), 0));
int maxArea = 0;
for(int i = 0;i < matrix.size();i++) {
for(int j = 0;j < matrix[0].size();j++) {
if(matrix[i][j] == '0') {
continue;
}
dp[i][j] = j == 0 ? 1 : dp[i][j - 1] + 1;
int width = dp[i][j];
for(int k = i;k >= i;k--) {
width = min(width, dp[k][j]);
maxArea = max(maxArea, width * (i - k + 1));
}
}
}
return maxArea;
}1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34int maximalRectangle (vector<vector<char>>& matrix) {
if(matrix.size() == 0) {
return 0;
}
int m = matrix.size(), n = matrix[0].size();
vector<int> left(n, 0);
vector<int> right(n, n);
vector<int> height(n, 0);
int maxArea = 0;
for(int i = 0; i < m; i++) {
int cur_left = 0, cur_right = n;
// update height
for(int j = 0; j < n; j++) {
if(matrix[i][j] == '1') height[j]++;
else height[j] = 0;
}
// update left
for(int j=0; j<n; j++) {
if(matrix[i][j]=='1') left[j]=max(left[j],cur_left);
else {left[j]=0; cur_left=j+1;}
}
// update right
for(int j = n - 1; j >= 0; j--) {
if(matrix[i][j] == '1') right[j] = min(right[j], cur_right);
else {right[j] = n; cur_right = j;}
}
// update area
for(int j = 0; j < n; j++) {
maxArea = max(maxArea, (right[j] - left[j]) * height[j]);
}
}
return maxArea;
}1
2
3
4
5输入:
nums1 = [1,2,3,0,0,0], m = 3
nums2 = [2,5,6], n = 3
输出: [1,2,2,3,5,6]1
2
3
4
5
6
7
8
9
10
11
12
13class Solution {
public:
void merge(vector<int>& nums1, int m, vector<int>& nums2, int n) {
int i = m - 1, j = n - 1;
for(int pos = m + n - 1; pos >= 0; pos--) {
if(i >= 0 && (j < 0 || nums1[i] >= nums2[j])) {
nums1[pos] = nums1[i--];
} else {
nums1[pos] = nums2[j--];
}
}
}
};1
2
3
4
5
6
7
8
9
10
11
12
13
14
15输入: 2
输出: [0,1,3,2]
解释:
00 - 0
01 - 1
11 - 3
10 - 2
对于给定的 n,其格雷编码序列并不唯一。
例如,[0,2,3,1] 也是一个有效的格雷编码序列。
00 - 0
10 - 2
11 - 3
01 - 11
2
3
4
5输入: 0
输出: [0]
解释: 我们定义格雷编码序列必须以 0 开头。
给定编码总位数为 n 的格雷编码序列,其长度为 2n。当 n = 0 时,长度为 20 = 1。
因此,当 n = 0 时,其格雷编码序列为 [0]1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19class Solution {
public:
vector<int> grayCode(int n) {
vector<int> ans;
if(n == 0) {
ans.push_back(0);
return ans;
}
ans.push_back(0);
ans.push_back(1);
for(int i = 1;i < n;i++) {
int num = 1 << i;
for(int j = ans.size() - 1;j >= 0;j--) {
ans.push_back(ans[j] + num);
}
}
return ans;
}
};