Celery's Blog

0%

LeetCode-Day18

发表于 更新于 Valine：

80. 删除排序数组中的重复项II

给定一个排序数组，你需要在原地删除重复出现的元素，使得每个元素最多出现两次，返回移除后数组的新长度。

不要使用额外的数组空间，你必须在原地修改输入数组并在使用 O(1) 额外空间的条件下完成。

示例 1:

1
2
3
4
5
给定 nums = [1,1,1,2,2,3],

函数应返回新长度 length = 5, 并且原数组的前五个元素被修改为 1, 1, 2, 2, 3 。

你不需要考虑数组中超出新长度后面的元素。

示例 2:

1
2
3
4
5
给定 nums = [0,0,1,1,1,1,2,3,3],

函数应返回新长度 length = 7, 并且原数组的前五个元素被修改为 0, 0, 1, 1, 2, 3, 3 。

你不需要考虑数组中超出新长度后面的元素。

思路：

原地删除肯定是双指针，一个指向遍历元素，一个指向可以写入的位置，后者的大小是小于等于前者的，关键在于题目条件的转换，如何实现限制最多两次的重复。

先不考虑边界的情况，只考虑中间的情况，假设当前的遍历位置为i，写指针的可写入位置为current +1，对于i处的值，其写入的条件时重复小于等于2次，我们考虑已经写入的最后两位current和current - 1，这两个位置的情况有两个，相等和不相等，首先考虑相等的情况，此时若i处的值和current - 1或者说与current处的值相同，那么i处的值肯定不能加入；然后考虑不相等的情况，即current - 1和current处值不相等，那么i处的值无论为什么，都满足题意，即可以加入，综上所述，当i处的值与current - 1的值不相等时，i处的值可以加入，其他情况均不能加入

接着考虑边界的情况，我们只需要考虑开始即可，开始时，前两个值无论等还是不等，都要原封不动的挪到新数组里，由于新数组就是在原数组上进行修改的，因此前两位直接不动即可，只需要修改遍历指针和写入指针就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        if(nums.size() <= 2) {
            return nums.size();
        }
        int current = 1;
        for(int i = 2;i < nums.size();i++) {
            if(nums[i] != nums[current - 1]) {
                nums[++current] = nums[i];
            }
        }
        return current + 1;
    }
};

84. 柱状图中的最大矩形

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

求在该柱状图中，能够勾勒出来的矩形的最大面积。

img

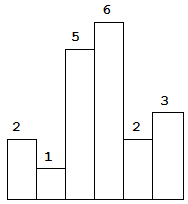
以上是柱状图的示例，其中每个柱子的宽度为 1，给定的高度为 [2,1,5,6,2,3]。

img

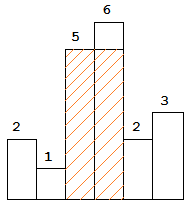
图中阴影部分为所能勾勒出的最大矩形面积，其面积为 10 个单位。

示例:

1
2
输入: [2,1,5,6,2,3]
输出: 10

方法一. 暴力

首先我们可以想到，两个柱子间矩形的高由他们之间最矮的柱子决定，如下图所示：

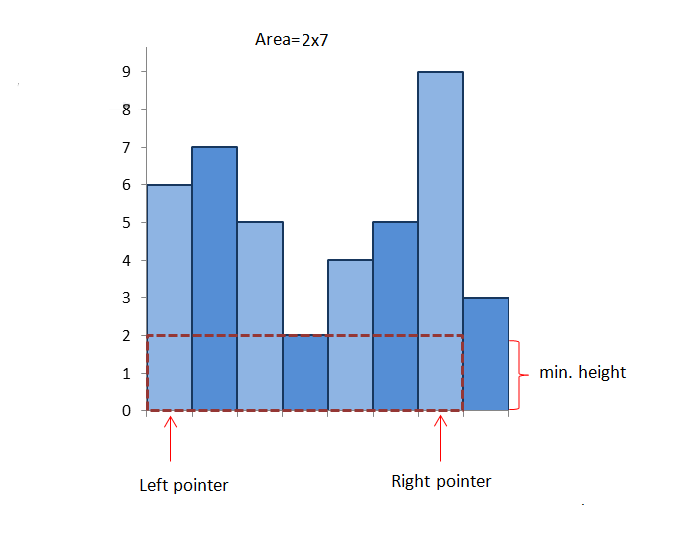
image.png

右移，我们可以考虑所有亮亮竹子之间形成的矩形面积，该矩形的高为他们之间最矮柱子的高度，宽为他们之间的距离，这样可以找到所要求的最大面积的矩形

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int largestRectangleArea(vector<int>& heights) {
    if(heights.size() == 1) {
        return heights[0];
    } else if(heights.size() == 0) {
        return 0;
    }
    int maxArea = 0;
    for(int i = 0;i < heights.size();i++) {
        for(int j = i; j < heights.size();j++) {
            int maxH = heights[i];
            for(int k = i;k <= j;k++) {
                maxH = min(maxH, heights[k]);
            }
            maxArea = max(maxArea, maxH * (j - i + 1));
        }
    }
    return maxArea;
}

复杂度分析：

  • 时间复杂度: O(n3)O(n^3)。我们需要使用O(n)O(n) 的时间找到O(n2)O(n^2)枚举出啦的所有柱子对之间的最矮柱子
  • 空间复杂度：O(1)O(1)。只需要常数空间的额外变量

方法二. 优化的暴力

算法：

我们可以基于方法1进行一点点修改来优化算法。我们可以用前一对柱子之间的最低高度来求出当前柱子对间的最低高度

即：minHeight=min(minHeight,heights[j])minHeight = min(minHeight, heights[j])，其中heights[j]heights[j]是第j个柱子的高度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
int largestRectangleArea(vector<int>& heights) {
    if(heights.size() == 1) {
        return heights[0];
    } else if(heights.size() == 0) {
        return 0;
    }
    int maxArea = 0;
    for(int i = 0;i < heights.size();i++) {
        int maxH = heights[i];
        for(int j = i; j < heights.size();j++) {
            maxH = min(maxH, heights[j]);
            maxArea = max(maxArea, maxH * (j - i + 1));
        }
    }
    return maxArea;
}

复杂度分析：

  • 时间复杂度： O(n2)O(n^2)，需要枚举所有可能的柱子对
  • 空间复杂度： O(1)O(1)，不需要额外的空间

然鹅…还是超时了…

方法三. 分治

通过观察，可以发现，最大面积矩形存在于以下几种可能

  • 确定了最矮柱子以后，矩形的宽尽可能往两边延伸
  • 在最矮柱子左边的最大面积矩形（子问题）
  • 在最矮柱子右边的最大面积矩形（子问题）

举个例子：

[6, 4, 5, 2, 4, 3, 9]
这里最矮柱子高度为 2 。以 2 为高的最大子矩阵面积是 2x7=14 。现在，我们考虑上面提到的第二种和第三种情况。我们对高度为 2 柱子的左边和右边采用同样的过程。在 2 的左边， 4 是最小的，形成区域为 4x3=12 。将左边区域再继续分，矩形的面积分别为 6x1=6 和 5x1=5 。同样的，我们可以求出右边区域的面积为 3x3=9, 4x1=4 和 9x1=9 。因此，我们得到最大面积是 16 。具体过程可参考下图：

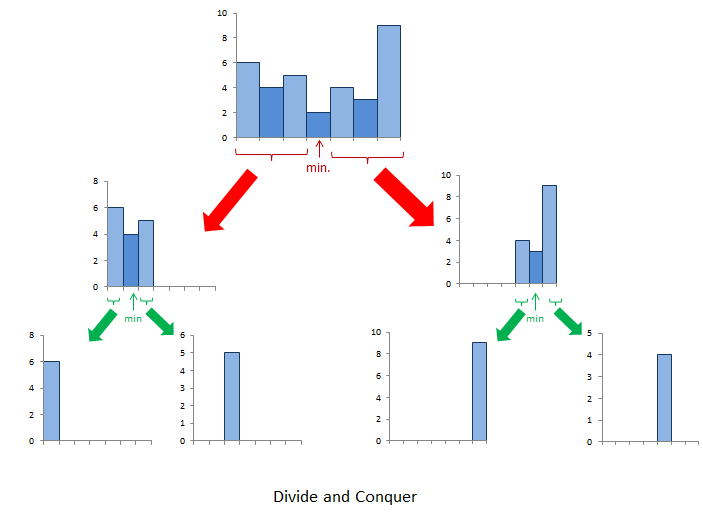
image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
int calculate(vector<int>& heights, int start, int end) {
    if(start > end) {
        return 0;
    }
    int midindex = start;
    for(int i = start;i <= end;i++) {
        midindex = heights[midindex] < heights[i] ? midindex : i;
    }
    return max(heights[midindex] * (end - start + 1), max(calculate(heights, midindex + 1, end), calculate(heights, start, midindex - 1)));
}

int largestRectangleArea(vector<int>& heights) {
    return calculate(heights, 0, heights.size() - 1);
}

复杂度分析：

  • 时间复杂度：

    • 平均开销：O(nlogn)O(nlogn)
    • 最坏情况：O(n2)O(n^2)。如果数组中的数字是有序的，分治算法将没有任何优化效果

  • 空间复杂度：O(n)O(n)。最坏情况下递归需要O(n)O(n)的空间

方法四. 优化的分治

可以观察到，方法三中大的问题被分解成更小的子问题来求解，所以分治方法会有一定程度的优化。但是如果数组本身是升序或者降序的，将没有任何优化作用，原因是我们每次都需要一个很大的O(n)O(n)级别的数组里找最小值。因此，最坏情况下总的时间复杂度变成了O(n2)O(n^2)。我们可以用线段树代替遍历来找到区间的最小值。单词查询复杂度就变成了O(logn)O(logn)

复杂度分析：

  • 时间复杂度：O(nlogn)O(nlogn)。对于长度为n的查询，线段树需要lognlogn的时间
  • 空间复杂度：O(n)O(n)。这是线段树的空间开销

方法五. 栈

算法

在这种方法中，我们维护一个栈。一开始，我们把-1放进栈的顶部来表示开始。初始化时，按照从左到右的顺序，我们不断将柱子的序号放进栈中，直到遇到相邻柱子呈下降关系，也就是a[i-1] > a[i]​。现在，我们开始将栈中的序号弹出，直到遇到stack[j]stack[j]满足a[stack[j]] <= a[i]。每次我们弹出下标的的时候，我们用弹出元素作为高形成的最大面积的矩形的高，宽是当前元素与stack[top - 1]之间的那些柱子。也就是当我们弹出stack[top]时，记当前元素在原数组中的下标为i，当前弹出元素为高的最大矩形面积为：

(i - stack[top - 1] - 1) * a[stack[top]]

更进一步，当我们达到数组的尾部时，我们将栈中的元素全部弹出栈。在弹出每一个元素时，我们用下面的式子来求面积：(stack[top] - stack[top - 1]) * a[stack[top]]。其中stack[top]表示刚刚被弹出的元素。因此，我们可以通过每次比较新计算的矩形面积来获得最大的矩形面积

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
    stack<int> st;
    st.push(-1);
    int maxArea = 0, size = heights.size();
    for(int i = 0;i < size;i++) {
        if(st.top() == -1 || heights[st.top()] <= heights[i]) {
            st.push(i);
        } else {
            while(st.top() != -1 && heights[st.top()] >= heights[i]) {
                int maxH = st.top();
                st.pop();
                maxArea = max(maxArea, heights[maxH] * (i - st.top() - 1));
            }
            st.push(i);
        }
    }
    while(st.top() != -1) {
        int maxH = st.top();
        st.pop();
        maxArea = max(maxArea, heights[maxH] * (size - st.top() - 1));
    }
    return maxArea;
    }
};

复杂度分析：

  • 时间复杂度： O(n)O(n)，n个数字每个会被压栈弹栈各一次
  • 空间复杂度：O(n)O(n)。用来存放栈中元素