Celery's Blog

0%

LeetCode-Day14

发表于 Valine：

42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

img

上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

示例:

1
2
输入: [0,1,0,2,1,0,1,3,2,1,2,1]
输出: 6

方法一：自己写的…先将height排序，然后从最高的两个柱子开始选取，然后遍历中间的部分，即可以装雨水的部分，已经装过水的地方做标记isTrue，不再重复接水。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
static bool cmp(pair<int, int>a, pair<int, int>b) {
    return a.second > b.second;
}

int trap(vector<int>& height) {
    if(height.size() < 2) {
        return 0;
    }
    vector<pair<int, int> > vec;
    for(int i = 0;i < height.size();i++) {
        pair<int, int> tmp(i, height[i]);
        vec.push_back(tmp);
    }
    sort(vec.begin(), vec.end(), cmp);
    for(vector<pair<int, int> >::iterator it = vec.begin();it != vec.end();it++) {
        cout << (*it).first << " " << (*it).second << endl;
    }
    bool isTrue[height.size()] = {0};
    int left, right, shorter, sum = 0;
    for(int i = 0; i < height.size() - 1;i++) {
        if(vec[i].first < vec[i + 1].first) {
            left = vec[i].first;
            right = vec[i + 1].first;
        } else {
            left = vec[i].first;
            right = vec[i + 1].first;
        }
        shorter = vec[i].second < vec[i + 1].second ? vec[i].second : vec[i + 1].second;
        for(int j = left + 1;j < right;j++) {
            if(isTrue[j] == false) {
                isTrue[j] = true;
                sum += (shorter - height[j]);
            }
        }
    }
    return sum;
}

方法二：动态编程

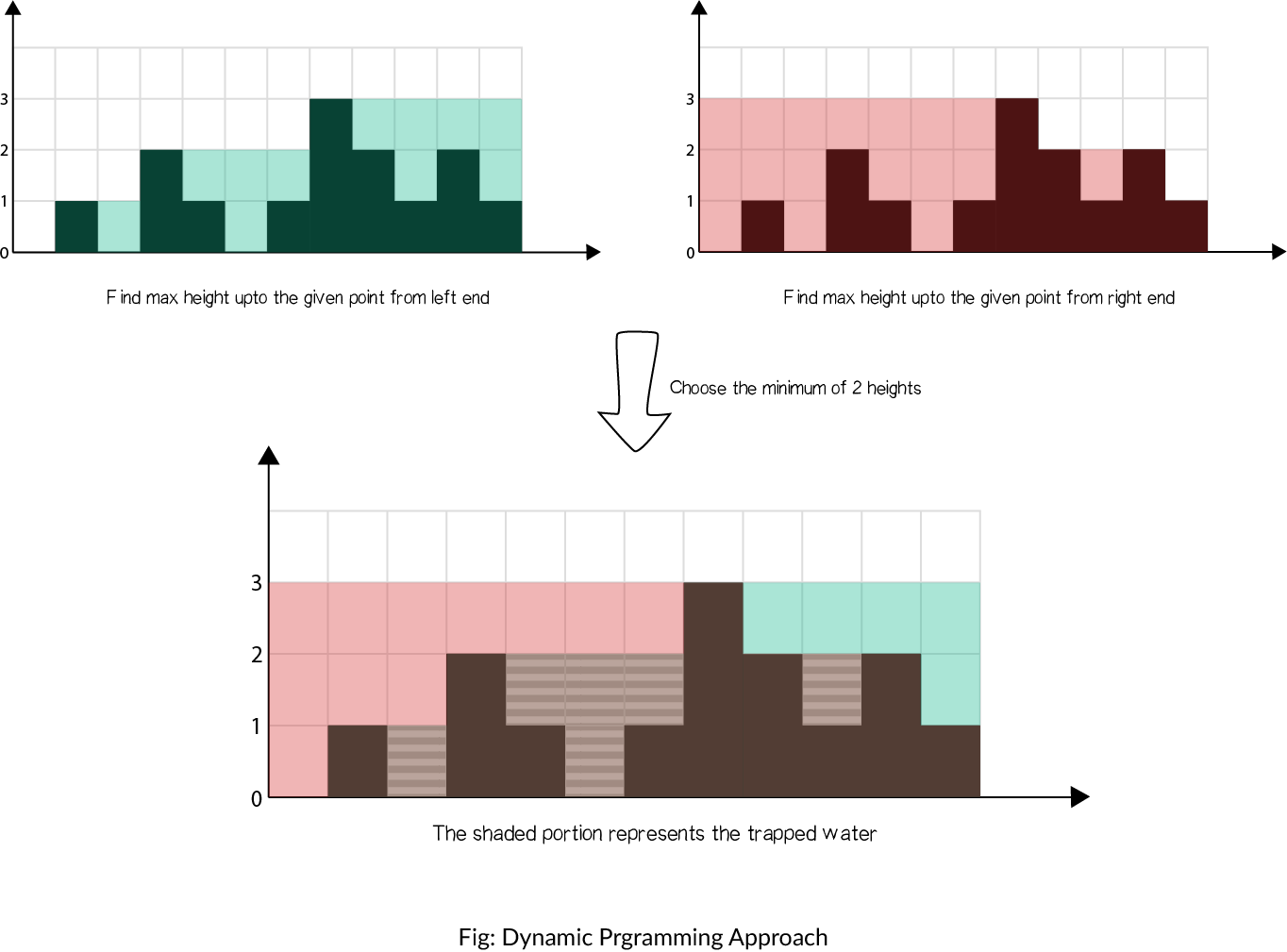
trapping_rain_water.png

算法

  • 找到数组中从下标 i 到最左端最高的条形块高度left_max。
  • 找到数组中从下标 i 到最右端最高的条形块高度right_max。
  • 扫描数组 height并更新答案：
    • 累加 min(max_left[i], max_right[i])-hright[i]到ans 上
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    int trap(vector<int>& height) {
        if(height.size() == 0) {
            return 0;
        }
        int ans = 0;
        int size = height.size();
        vector<int> left_max(size), right_max(size);
        left_max[0] = height[0];
        for(int i = 1;i < size;i++) {
            left_max[i] = max(height[i], left_max[i - 1]);
        }
        right_max[size - 1] = height[size - 1];
        for(int i = size - 2;i >= 0;i--) {
            right_max[i] = max(height[i], right_max[i + 1]);
        }
        for(int i = 0;i < size - 1;i++) {
            ans += (min(left_max[i], right_max[i]) - height[i]);
        }
        return ans;

    }
};

方法三：使用双指针

和方法 2 相比，我们不从左和从右分开计算，我们想办法一次完成遍历。
从动态编程方法的示意图中我们注意到，只要right_max[i]>left_max[i]（元素 0 到元素 6），积水高度将由 left_max 决定，类似地left_max[i] > right_max[i]（元素 8 到元素 11）。
所以我们可以认为如果一端有更高的条形块（例如右端），积水的高度依赖于当前方向的高度（从左到右）。当我们发现另一侧（右侧）的条形块高度不是最高的，我们则开始从相反的方向遍历（从右到左）。
我们必须在遍历时维护 left_max 和 right_max ，但是我们现在可以使用两个指针交替进行，实现 1 次遍历即可完成。

算法如下

img

img

img

img

img

img

img

img

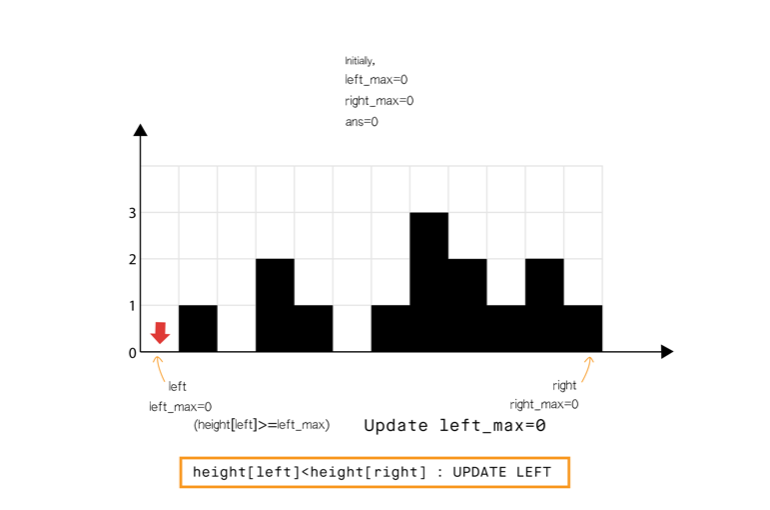
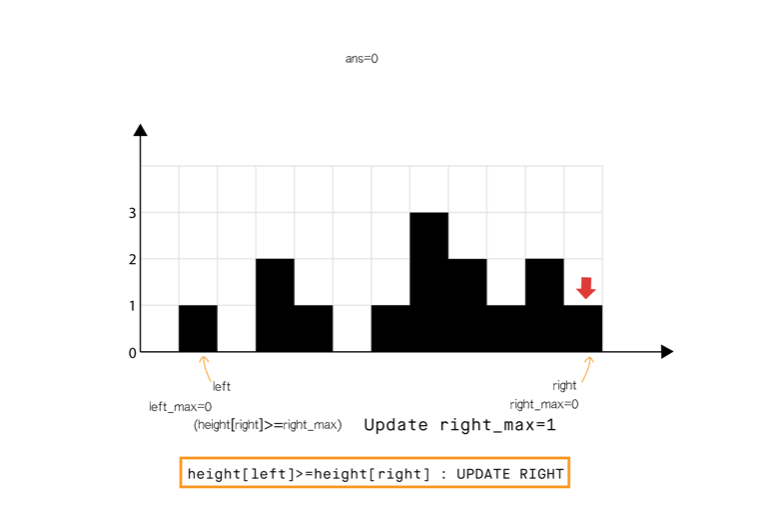
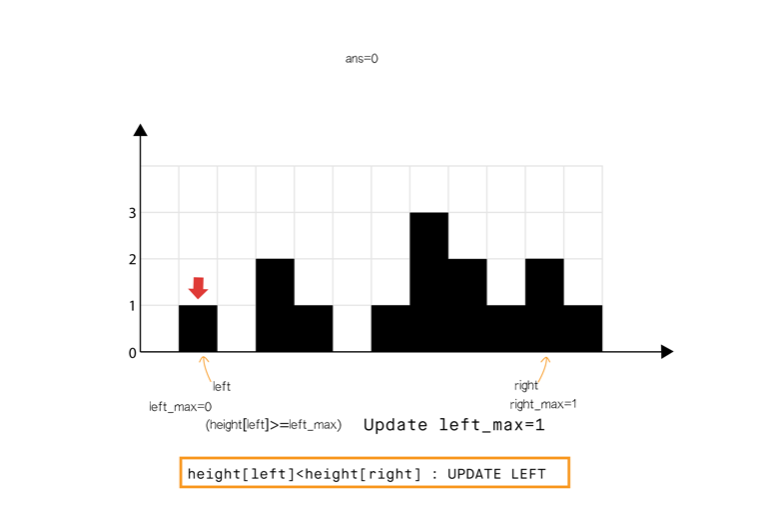
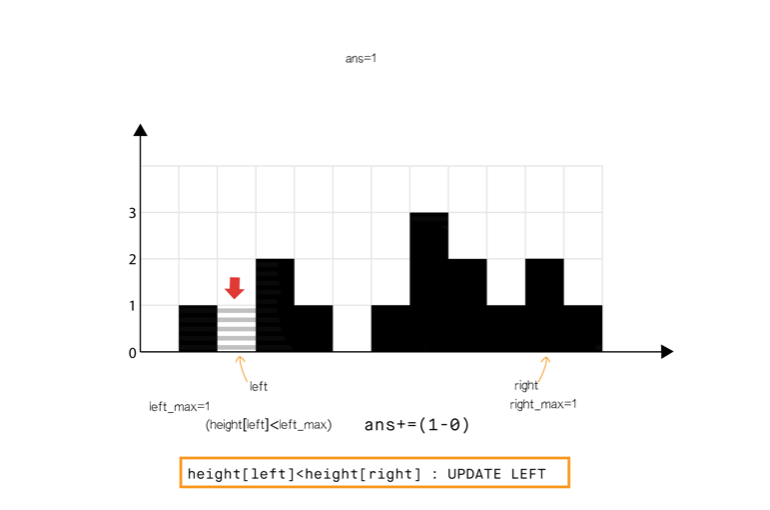
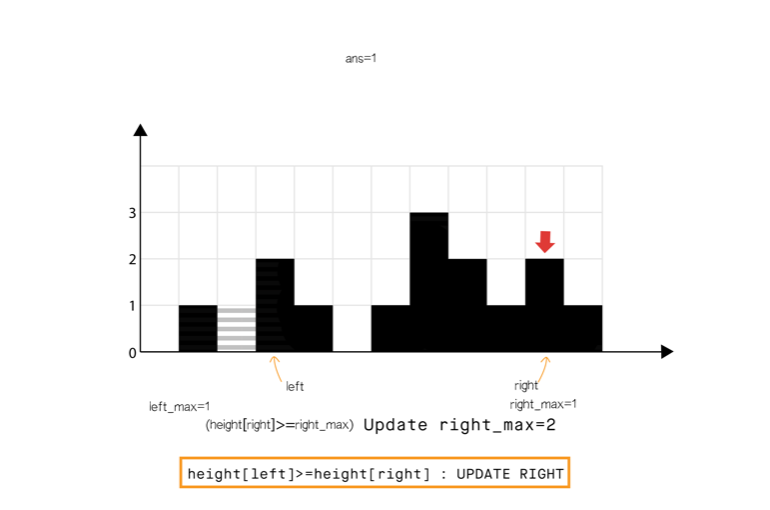
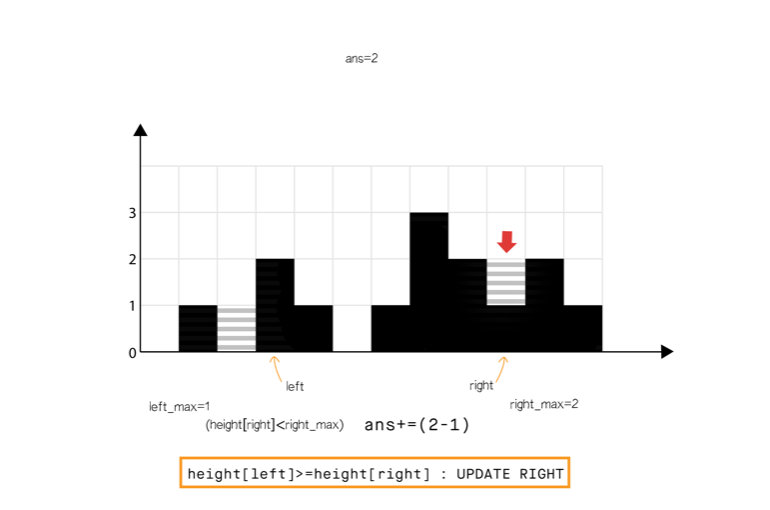
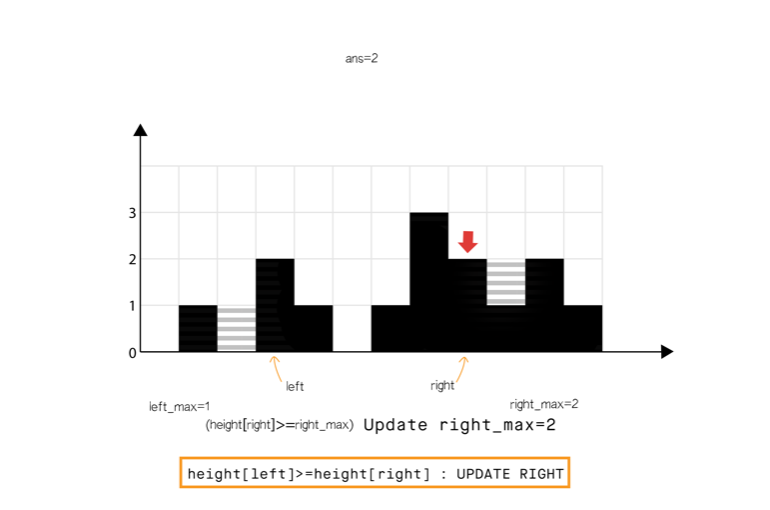
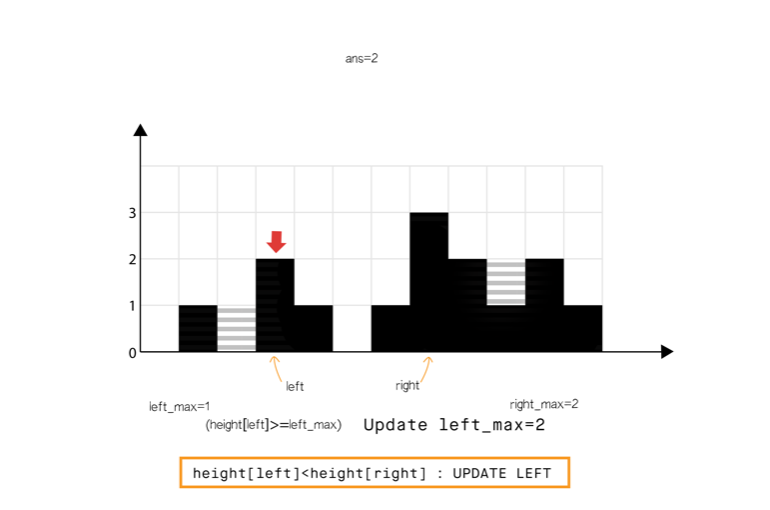
省略…

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
public:
    int trap(vector<int>& height) {
        int left = 0, right = height.size() - 1;
        int ans = 0;
        int left_max = 0, right_max = 0;
        while(left  < right) {
            if(height[left] < height[right]) {
                height[left] >= left_max ? (left_max = height[left]) : ans += (left_max - height[left]);
                ++left;
            } else {
                height[right] >= right_max ? (right_max = height[right]) : ans += (right_max - height[right]);
                right--;
            }
        }
        return ans;
    }
};

45. 跳跃游戏（贪心算法）

给定一个非负整数数组，你最初位于数组的第一个位置。

数组中的每个元素代表你在该位置可以跳跃的最大长度。

你的目标是使用最少的跳跃次数到达数组的最后一个位置。

示例:

1
2
3
4
输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
     从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

说明:

假设你总是可以到达数组的最后一个位置。

一开始的想法是，利用动态规划（不知道算不算），当前位于 i 的位置，然后nums[i]表示当前可以往下跳的范围。更新jumps数组中下标为i ~ i + nums[i]范围的值。（jumps数组表示从起始位置跳到当前位置所需要的最少的跳跃数）。然后返回jumps数组的最后一个元素

1
2
3
4
5
6
7
8
9
int jump(vector<int>& nums) {
    int jumps[nums.size()] = {0};
    for(int i = 0;i < nums.size() - 1;i++) {
        for(int j = 1;i + j < nums.size() && j < nums[i];j++) {
            jumps[i + j] = jumps[i] + 1 < jumps[i + j] ? jumps[i] + 1 : jumps[i + j];
        }
    }       
    return jumps[nums.size() - 1];
}

不幸的是，超时了…

所以需要其他的解决方法了…

贪心算法出场了！！！

贪心算法，我们每次在可跳范围内选择可以使得跳的更远的位置。

如下图，开始的位置是 2，可跳的范围是橙色的。然后因为 3 可以跳的更远，所以跳到 3 的位置。

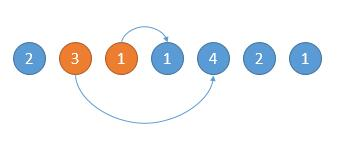
image.png

如下图，然后现在的位置就是 3 了，能跳的范围是橙色的，然后因为 4 可以跳的更远，所以下次跳到 4 的位置。

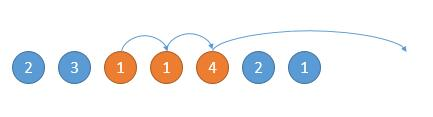
image.png

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
class Solution {
public:
    int jump(vector<int>& nums) {
        int i = 0, count = 0;
        while(i < nums.size() - 1) {
            int index;
            int far = 0;
            for(int j = 1;j <= nums[i];j++) {
                if(i + j >= nums.size() - 1) {
                    return count + 1;
                }
                if(j + nums[i + j] > far) {
                    index = i + j;
                    far = j + nums[i + j];
                }
            }
            i = index;
            count++;
        }
        return count;
    }
};

47. 全排列II

给定一个可包含重复数字的序列，返回所有不重复的全排列。

示例:

1
2
3
4
5
6
7
输入: [1,1,2]
输出:
[
  [1,1,2],
  [1,2,1],
  [2,1,1]
]

方法：回溯+剪枝（剪枝的效果是去重复）

下面这段话是解决有重复元素的序列的排列问题的关键：

当数组中有重复元素的时候，可以先将数组排序，排序以后在递归的过程中可以很容易发现重复的元素。当发现重复元素的时候，让这一个分支跳过，以达到“剪枝”的效果，重复的排列就不会出现在结果集中。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
public:
    void findPermute(vector<int>& nums, vector<int>& temp, vector<vector<int> >& ans, int index, bool isused[]) {
        if(index == nums.size()) {
            ans.push_back(temp);
            return ;
        }
        for(int i = 0;i < nums.size();i++) {
            if(!isused[i]) {
                if(i > 0 && nums[i] == nums[i - 1] && !isused[i - 1]) {
                    continue;
                }
                temp.push_back(nums[i]);
                isused[i] = true;
                findPermute(nums, temp, ans, index + 1, isused);
                temp.pop_back();
                isused[i] = false;
            }
        }
    }

    vector<vector<int> > permuteUnique(vector<int>& nums) {
        bool isused[nums.size()] = {0};
        vector<int> temp;
        vector<vector<int> > ans;
        if(nums.size() == 0) {
            return ans;
        } else if(nums.size() == 1) {
            ans.push_back(nums);
            return ans;
        }
        sort(nums.begin(), nums.end());
        findPermute(nums, temp, ans, 0, isused);
        return ans;
    }
};

这个代码片段是关键：

1
2
3
if(i > 0 && nums[i] == nums[i - 1] && !isused[i - 1]) {
	continue;
}

在进入一个新的分支之前，看看最后一个数是不是和之前一样，如果这个数和之前的数一样，并且之前的数还未使用过，那接下来如果走这个分支，就回使用到之前那个和当前一样的数，就回发生重复，此时分支和之前的分支一模一样