11. 盛最多水的容器
给定 n 个非负整数 a1,a2,…,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2

示例:
1
2
| 输入: [1,8,6,2,5,4,8,3,7]
输出: 49
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| class Solution {
public:
int maxArea(vector<int>& height) {
int len = height.size();
int left = 0, right = len - 1;
int max = 0, temp = 0;
int minHeight;
while(left != right) {
minHeight = height[left] < height[right] ? height[left++] : height[right--];
temp = minHeight * (right - left + 1);
if(temp > max) {
max = temp;
}
}
return max;
}
};
|
解释:
这里采用的是双指针法
这种方法背后的思路在于,两线段之间形成的区域总是会受到较短的那条长度的限制。此外,两条线段距离越远,得到的面积就会越大。
所以,我们在由线段构成的数组中使用两个指针,一个放在开始,一个放在末尾。此外,我们会使用变量 max 来持续存储到目前为止所获得的最大面积。 在每一步中,我们会找出指针所指向的两条线段形成的区域,更新 max,并将指向较短线段的指针向较长线段那端移动一步。
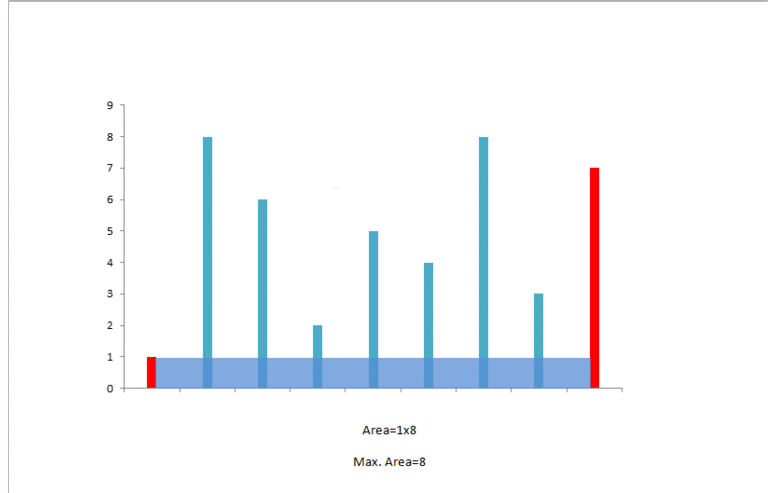
这种方法如何工作?
最初我们考虑由最外围两条线段构成的区域。现在,为了使面积最大化,我们需要考虑更长的两条线段之间的区域。如果我们试图将指向较长线段的指针向内侧移动,矩形区域的面积将受限于较短的线段而不会获得任何增加。但是,在同样的条件下,移动指向较短线段的指针尽管造成了矩形宽度的减小,但却可能会有助于面积的增大。因为移动较短线段的指针会得到一条相对较长的线段,这可以克服由宽度减小而引起的面积减小。
12.整数转罗马数字
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public:
string intToRoman(int num) {
int values[] = {1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1};
string reps[] = {"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"};
string res;
for(int i = 0; i < 13; i++) {
while(num >= values[i]) {
num -= values[i];
res += reps[i];
}
}
return res;
}
};
|

