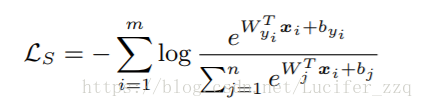center loss

Center Loss

一. 简介

论文链接：http://ydwen.github.io/papers/WenECCV16.pdf

二. 为什么要使用Center Loss？

简单的来说，我们在做分类的时候，不光需要学得separable的特征，更想要这些特征是discriminative的，这就意味着我们需要在loss上做更多的约束。

仅仅使用softmax作为监督信号的输出处理就只能做到seperable而不是discriminative，如下图:

三. 如何使学到的特征差异化更大——Center Loss

融合Softmax Loss与Center loss

Softmax Loss（保证类之间的feature距离最大）与Center Loss（保证类内的feature距离最小，更接近于类中心）

m是mini-batch、n是class。在Lc公式中有一个缺陷，就是$C_{y_{i}}$是i这个样本对应的类别yi所属于的类中心C∈ Rd，d代表d维。

理想情况下，Cyi需要随着学到的feature变化而实时更新，也就是要在每一次迭代中用整个数据集的feature来算每个类的中心。

但这显然不现实，做以下两个修改：

1、由整个训练集更新center改为mini-batch更改center

2、避免错误分类的样本的干扰，使用scalar α 来控制center的学习率

因此求算梯度的公式如下：

即：当yi = j，也就是mini-batch中某一个sample是对应要更新的那一个类的center的时候就累加起来除以某类的个数+1。

最终loss联立起来如上图，λ用于平衡softmax loss与center loss，越大则区分度 越大，如下图效果：

四. Center Loss的实现

pytorch实现：https://github.com/jxgu1016/MNIST_center_loss_pytorch

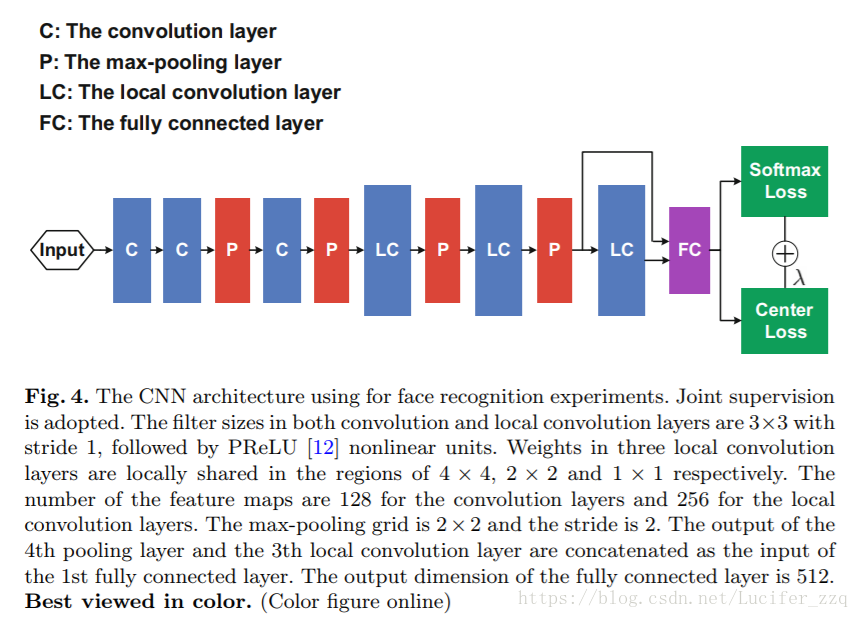
• 网络结构

即在特征层输出（classification前最后一层）引入center loss：

fully-connected 和 local-connected

判断fully-connected的方法：

• 对于neuron的链接（点对点的链接）都是fully connected（这里其实就是MLP）

• 对于有filter的network，不是看filter的size，而是看output的feature map的size。如果output feature map的size还是1 * 1 * N的话，这个layer就是fully connected layer

  解释第二个判断方法：

  • 1 * 1的filter size不一定是fully connected。比如input size是10 * 10 * 100， filter size是1 * 1 * 100， 重复50次，则该layer的总weights是：1 * 1 * 100 * 50
  • 1 * 1的filter size如果要是 fully connected， 则input size必须是1 * 1
  • input size是10x10的时候却是fully connected的情况：这里我们的output size肯定是1x1，且我们的filter size肯定是10x10。

  总结：filter size等于input size则是fully connected

综上：

• fully connected没有weight share
• 对于neuron的连接（点对点的链接）都是fully connected（MLP——多层感知器）
• Convolution中当filter size等于input size时，就是fully connected，此时的output size为1 * 1 * N
• 当1 *1不等于input size时，1 * 1一样具备weights share的能力。