NormFace

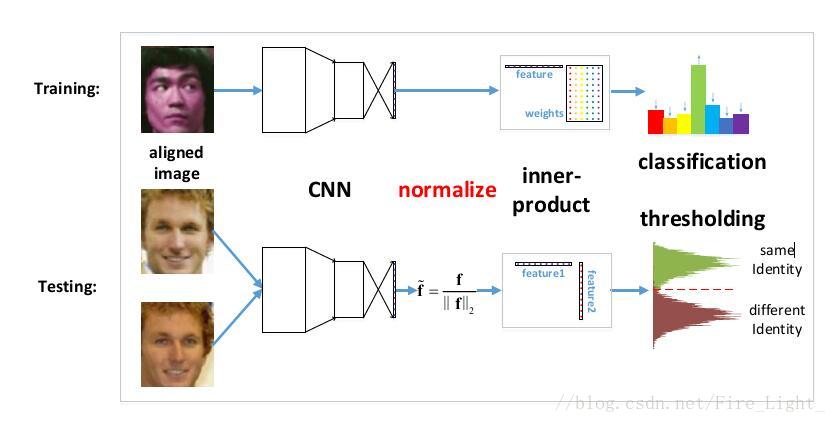
人脸识别：NormFace

参考链接：https://blog.csdn.net/wfei101/article/details/82890444

提出问题

之前的人脸识别工作，在特征比较阶段，通常使用的都是特征的余弦距离

$cos \theta = \frac {a * b} {||a|| ||b||}$

而余弦距离等价于L2归一化后的内积，也等价于L2归一化后的欧氏距离（欧氏距离表示超球面上的弦长，两个向量之间的夹角越大，弦长也越大）

然而，实际上训练的时候用的都是没有L2归一化的内积

关于这一点，可以这样解释，softmax函数是：

$P_{k}= \frac {e^{W_{k}x}} {\sum_{j=0}^{d} e^{W_{j}x}}$

可以理解为$W_{k}$ 和特征向量 $x$的内积越大，x属于第k类概率也就越大，训练过程就是最大化x与其标签项所对应项的权值$W_{label(x)}$的过程

也就是说在训练时使用的距离度量与在测试时使用的度量是不一样的

测试时是否需要归一化？

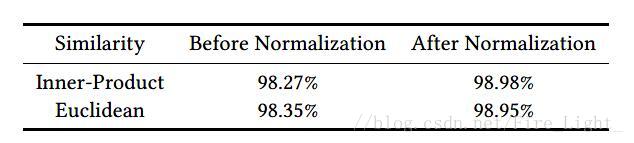
事实证明，进行人脸验证时，使用归一化后的内积或者欧氏距离效果会优于直接计算两个特征向量的内积或者欧氏距离，实验结果如下

• 注意这个Normalization不同于batch normalization，一个是对L2翻书进行归一化，一个是均值归0，方差归1

那么是否可以直接在训练时也对特征向量归一化？

针对上面的问题，作者设计实验，通过归一化Softmax所有的特征和权重来创建一个cosine layer，实验结果是网络不收敛了。

本论文要解决的四大问题：

• 为什么在测试时必须要归一化？
• 为什么直接优化余弦相似度会导致网络不收敛？
• 怎么样使用softmaxloss优化余弦相似度？
• 既然softmax loss在优化余弦相似度时不能收敛，那么其他的损失函数可以收敛吗？

L2归一化

为什么要归一化

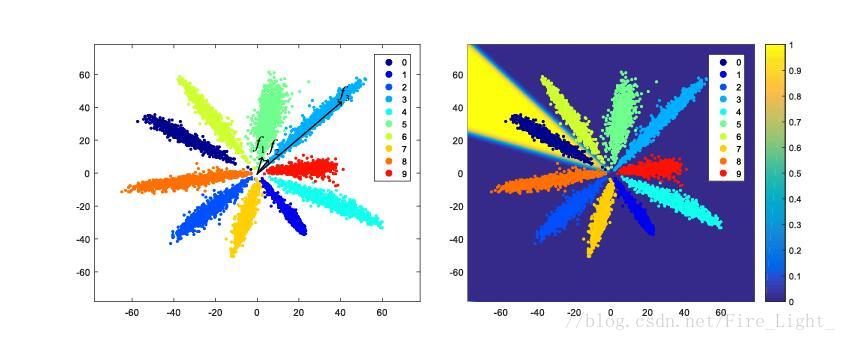
全连接层特征降至二维的MNIST特征图

左图中，f2f3是同一类的两个特征，但是可以看到f1和f2的距离明显小于f2和f3的距离，因此，加入不对特征进行归一化再比较距离的话，可能就会误判f1f2为同一类

为什么特征会呈辐射状分布？

Softmax实际上是一种（Soft）软的max（最大化）操作,考虑Softmax的概率

$P_{i}(f)= \frac {e^{W_{i}^{T}f}} {\sum_{j=1}^{n} e^{W_{j}^{T}f}}$

假设是一个十个分类问题，那么每个类都会对应一个权值向量W0,W1…W9,某个特征f会被分为哪一类，取决f和哪一个权值向量的内积最大。

也就是说，靠近W0的向量会被归为第一类，靠近W1的向量会归为第二类，以此类推。网络在训练过程中，为了使得各个分类更明显，会让各个权值向量W逐渐分散开，相互之间有一定的角度，而靠近某一权值向量的特征就会被归为相应的类别，因此特征最终会呈辐射状分布。

如果添加了偏置，结果会是怎么样的呢？

$L_{s}= - \frac{1}{m} \sum_{i = 1}^{m} log\frac {e^{W_{y_{i}}^{T} f_{i} + b_{y_{i}}}} {\sum_{j=1}^{n} e^{W_{j}^{T}f_{i} + b_{j}}}$

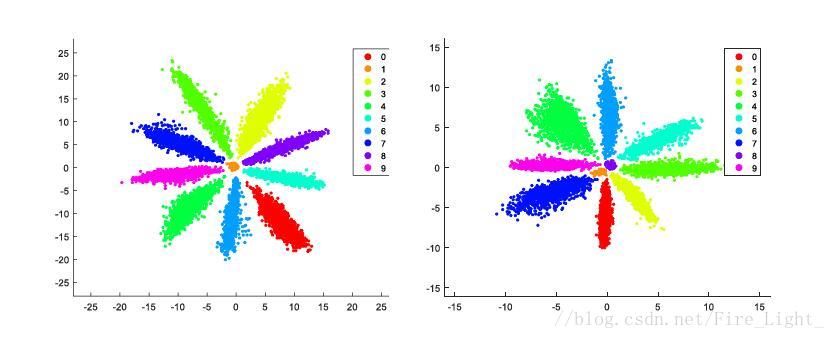
如果添加了骗纸，不同类的b不同，则会造成有的类w角度近似相等，而依据b来区分的情况。如下图：

在这种情况下，如果再对w进行归一化，那个中间这些类会散步在单位圆上各个方向，造成错误分类。

所以添加偏置对我们通过余弦距离来分类没有帮助，弱化了网络的学习能力，所以我们不添加偏置

网络为何不收敛？