Speed Up Training
主要包括以下几种模式:
- Stochastic Gradient Descent (SGD)
- Momentum
- AdaGrad
- RMP Prop
- Adam
Stochastic Gradient Descent (SGD)

想象红色方块使我们要训练的data,如果用普通的训练方法,就需要重复不断的把整套数据放入神经网络NN训练,这样消耗的计算资源会很大
SGD的正确打开方式:将这些数据拆分成小批小批的,然后再分批不断放入NN中计算。每次使用批数据,虽然不能反映整体数据情况,不过却很大程度上加速了NN的训练过程,而且也不会丢失太多准确率
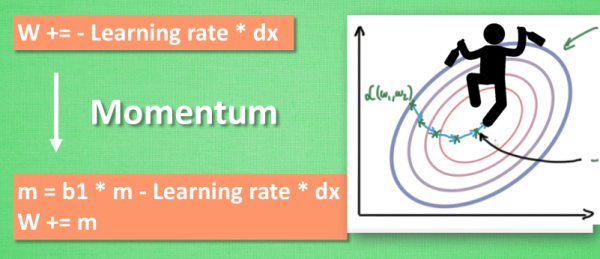
Momentum
大多数途径是在更新神经网络参数那一步上东东手脚。传统的参数W的更新是把原始的W累加上一个负的学习效率(Learning Rate)乘以校正值(dx)。这种方法可能会让学习的过程曲折无比,看起来像喝醉的人回家时,摇摇晃晃走了很多弯路
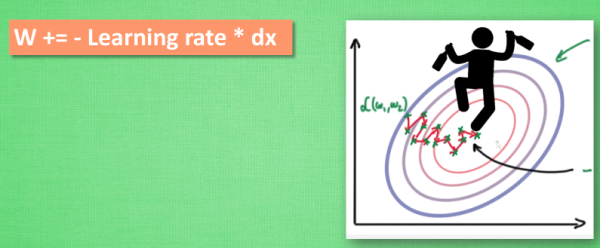
所以我们把这个人从平地上放到了一个斜坡上, 只要他往下坡的方向走一点点, 由于向下的惯性, 他不自觉地就一直往下走, 走的弯路也变少了. 这就是 Momentum 参数更新
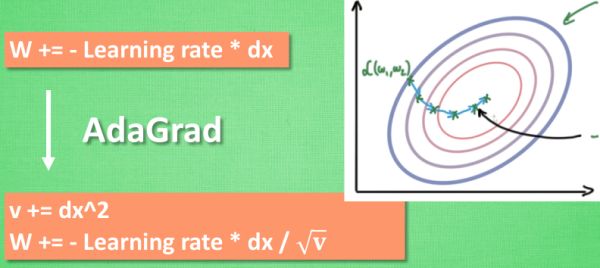
AdaGrad
这种方法是在学习率上面动手脚, 使得每一个参数更新都会有自己与众不同的学习率, 他的作用和 momentum 类似, 不过不是给喝醉酒的人安排另一个下坡, 而是给他一双不好走路的鞋子, 使得他一摇晃着走路就脚疼, 鞋子成为了走弯路的阻力, 逼着他往前直着走. 他的数学形式是这样的.
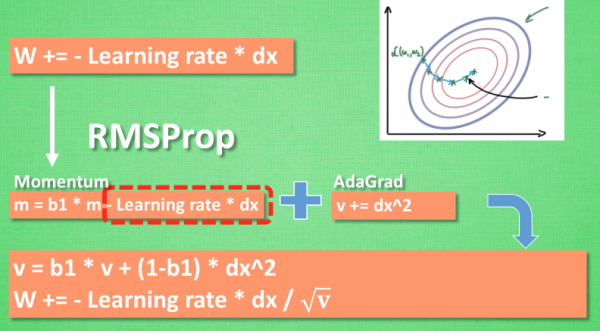
RMSProp
有了 momentum 的惯性原则 , 加上 adagrad 的对错误方向的阻力, 我们就能合并成这样. 让 RMSProp同时具备他们两种方法的优势. 不过还没把 Momentum合并完全, RMSProp 还缺少了 momentum 中的 这一部分. 所以, 我们在 Adam 方法中补上了这种想法.
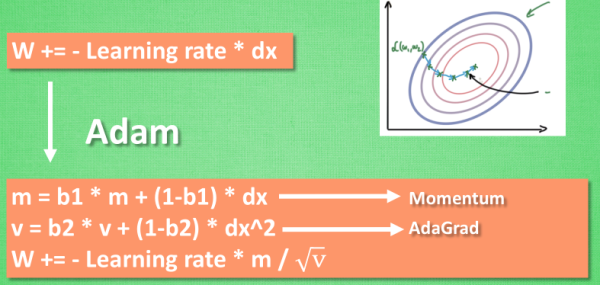
Adam
计算m 时有 momentum 下坡的属性, 计算 v 时有 adagrad 阻力的属性, 然后再更新参数时 把 m 和 V 都考虑进去. 实验证明, 大多数时候, 使用 adam 都能又快又好的达到目标, 迅速收敛. 所以说, 在加速神经网络训练的时候, 一个下坡, 一双破鞋子, 功不可没.
源代码:
1 | import torch |
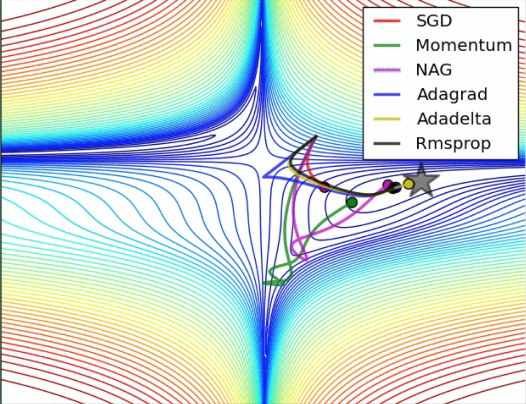
最后的图表: